If An is the area bounded by y=x and y=xn,n∈N, then A2.A3…An=
A
1n(n+1)
B
12nn(n+1)
C
12n−1n(n+1)
D
12n−2n(n+1)
Video Solution
Text Solution
The correct Answer is:D
y=x intersect y=xn at (0,0)and(1,0) for all n∈N
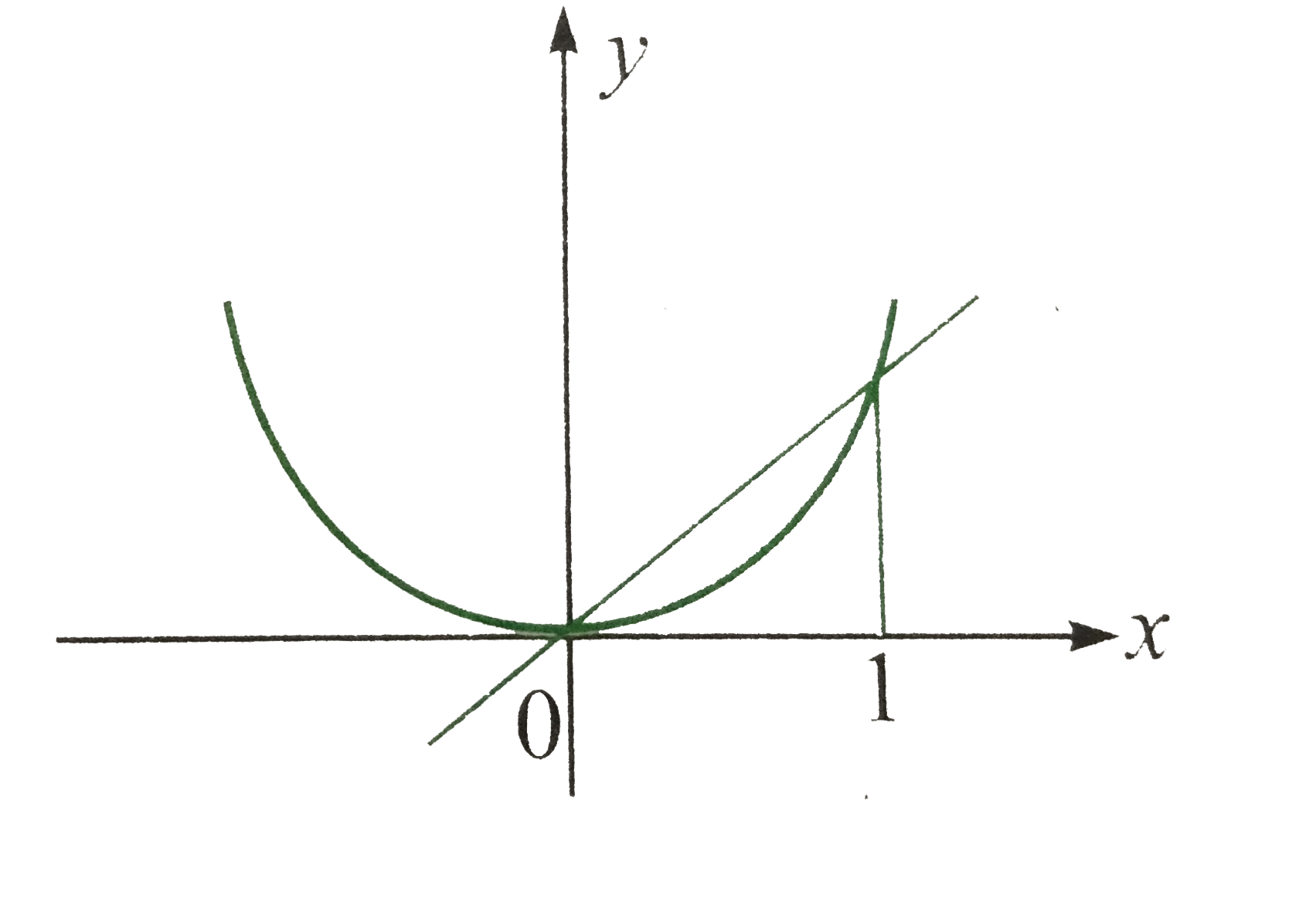
Area An=1∫0(x−xn)dx
=[x22−xn+1n+1]10
=12−1n+1
=n−12(n+1)
Thus, A2⋅A3⋅A4....An=12n−1(13⋅24⋅35...n−1n+1)
=12n−2.n(n+1)
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Let a1,a2,a3 …. an be in G.P. If the area bounded by the curve y2=4anX and y2=4an(an−x) be An, then the sequence A1,A2,A3…….An are in
AA.PBG.PCH.PDnone of theseA1,A2,A3,……,An and B1,B2,B3,….,Bn are non-singular square matrices of order n such that A1B1=In,A2B2=In,A3B3=In,……AnBn=In then(A1A2A3…..An)−1 = ______.
AB1B2B3…BnBB−11B−12B−13…B−1nCBnBn−1Bn−2….B1DBn−1Bn−1−1Bn−2−1...B−11If A1,A2,A3 denote respectively the areas of an inscribed polygon of 2n sides , inscribed polygon of n sides and circumscribed poylgon of n sides ,then A1,A2,A3 are in
AA.P.BG.P.CH.P.Dnone of these
If An be the area bounded by the curve y=(tanxn) ands the lines x=0, y=0, x=π/4 Prove that for n>2. , An+An+2=1n+1 and deduce 12n+2<An<12n−2
View SolutionB={an:n∈N,an+1=2ananda1=3}
View SolutionIf A1,A2,.....An are independent events associated with a random experiment; then P(A1∩A2∩.......∩An)=P(A1)P(A2).......P(An)
View SolutionIf f(x+y)=f(x)f(y) for all x and y,f(1)=2 and an=f(n),n∈N, then the equation of the circle having (a1,a2) and (a3,a4) as the ends of its one diameter
View SolutionIf n is a positive integer and
(1+x+x2)n=a0+a1x+….+a2nx2n.
Then, show that, a20−a21+….a22n=an.
View Solution