The area of the region bounded by $x^{2} + y^{2} - 2 x - 3 = 0 and y = | x | + 1$ is

A

$\frac{π}{2} - 1$ sq. units

B

$2 π$ sq. units

C

$4 π$ sq. units

D

$π / 2$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

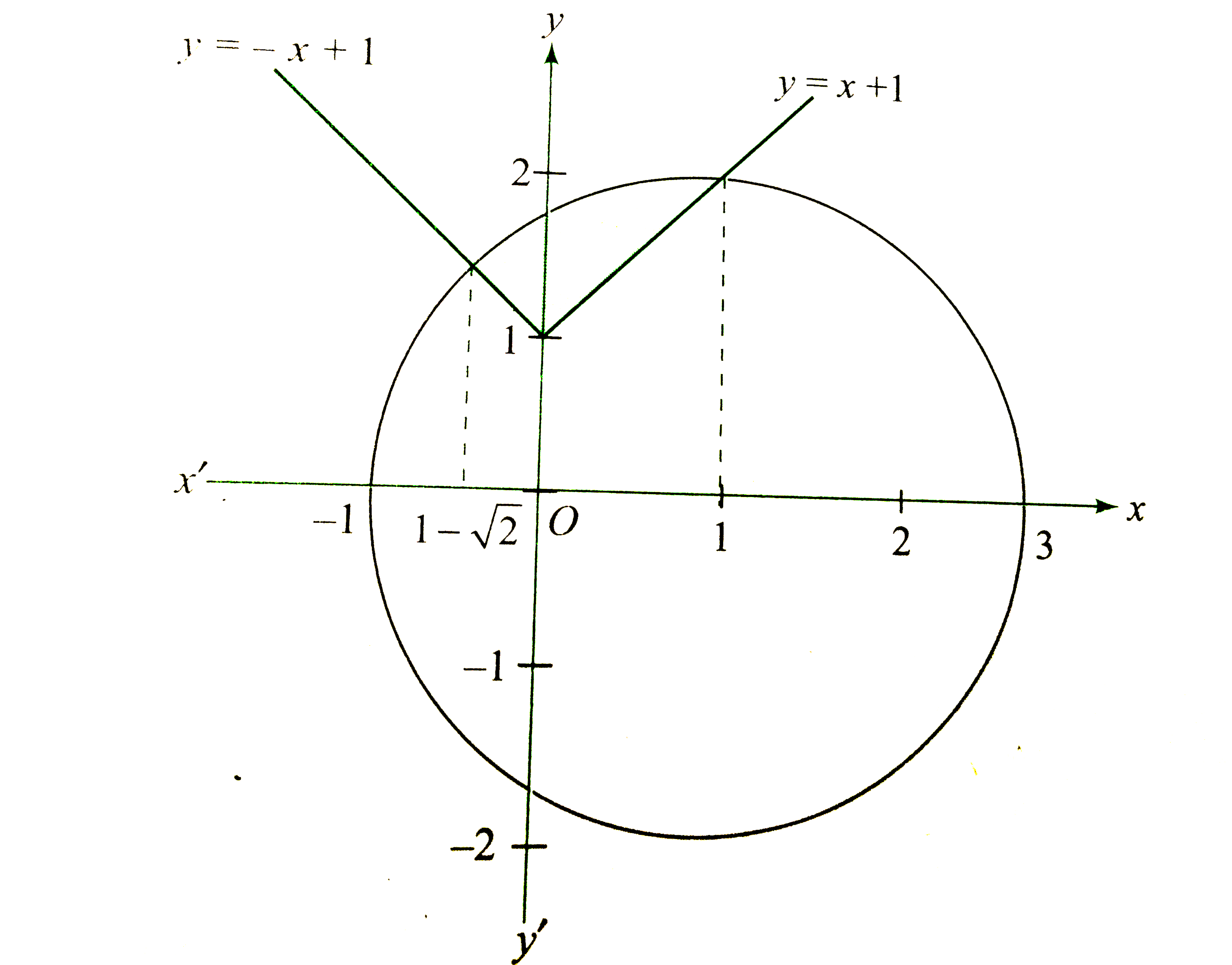
$x^{2} + y^{2} - 2 x - 3 = 0$
$or {(x - 1)}^{2} + y^{2} = 4$
$A = 0 \int 1 - \sqrt{2} (\sqrt{4 - {(x - 1)}^{2}} - (- x + 1)) d x + 1 \int 0 (\sqrt{4 - {(x - 1)}^{2}} - (x + 1)) d x$
$= \frac{x - 1}{2} \sqrt{4 - {(x - 1)}^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x - 1}{2} + \frac{x^{2}}{2} - x {∣ ∣ ∣}_{1 - \sqrt{2}}^{0} + \frac{x - 1}{2} \sqrt{4 - {(x - 1)}^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x - 1}{2} - \frac{x^{2}}{2} - x {∣ ∣ ∣}_{0}^{1}$
$= (- \frac{\sqrt{3}}{2} - \frac{π}{3}) - (\frac{- \sqrt{2}}{2} \sqrt{2} - \frac{π}{2} + \frac{3 - 2 \sqrt{2}}{2} - 1 + \sqrt{2}) + (- \frac{1}{2} - 1) - (- \frac{\sqrt{3}}{2} - \frac{π}{3})$
$= - (- 1 - \frac{π}{3} + \frac{3}{2} - \sqrt{2} - 1 + \sqrt{2}) - \frac{3}{2}$
$= \frac{π}{2} - 1$ sq. units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bounded by $x^{2} + y^{2} - 2 y - 3 = 0 and y = | x | + 1,$ is
A $π$
B $2 π$
C $4 π$
D $π / 2$
The area of the region bounded by $y = x^{2}$ and $y = - x^{2} + 2$ is
A $\frac{5}{3}$
B $\frac{4}{3}$
C $\frac{8}{3}$
D1
The area of the region bounded by $x = y^{2} - y$ and Y-axis is
A $\frac{3}{2}$ sq. units
B $\frac{2}{3}$ sq. units
C $\frac{5}{3}$ sq. units
D $\frac{1}{6}$ sq. units

CENGAGE-AREA-Exercise (Single)

Home
Ask Doubt
Profile