Find the area enclosed between the curves: y=loge(x+e),x=loge(1y) & the x-axis.
A
2 sq. units
B
1 sq. units
C
4 sq. units
D
None of these
Video Solution
Text Solution
The correct Answer is:A
y=loge(x+e),x=loge(1y)ory=e−x.
For y=loge(x+e), Shift the graph of y=logex,e units to the left hand side.
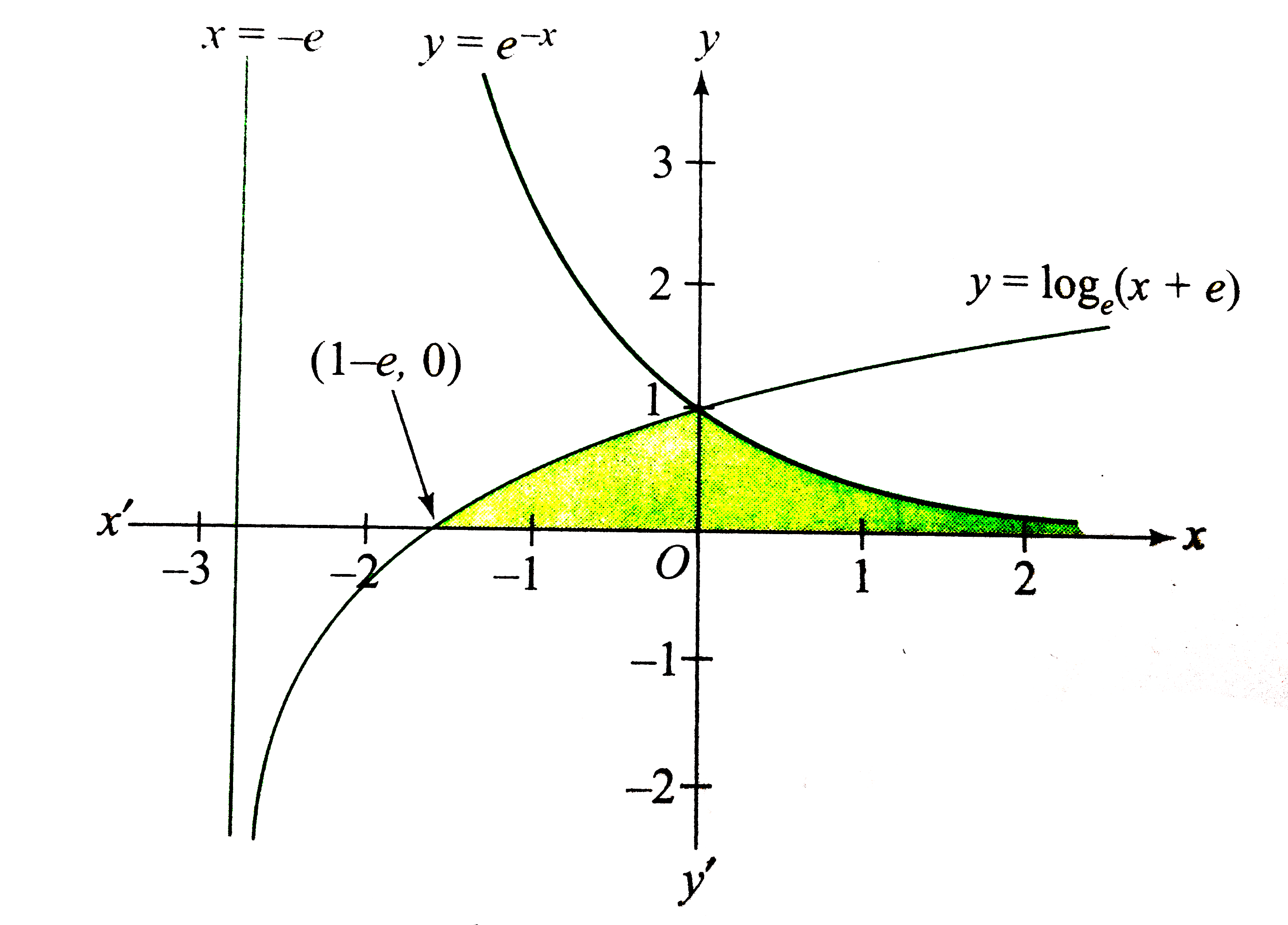
Required area =0∫1−eloge(x+e)dx+∞∫0e−xdx
=|xloge(x+e)|01−e−0∫1−exx+edx−∣∣e−x∣∣∞0
=1−e∫0(1−ex+e)dx−e∞+e0
=|x−elog(x+e)|1−e0−0+1
=1−e+eloge+1=2 sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
The area enclosed between the curve y=loge(x+e) and the coordinate axes is
A3B4C1D2The area enclosed between the curve y=loge(x+e) and the coordinate axes is
A4 sq unitsB3 sq unitsC2 sq unitsD1 sq unitThe area (in sqaure units) of the region enclosed by the curves y=x,x=e,y=1x and the positive x-axis is
A12B1C32D52
The area enclosed between the curve y=loge(x+e) and the coordinate axes is
View SolutionFind the area enclosed between the curve y=logx1, X-axis and ordinates x=12andx=32.
View SolutionThe curve x=logy+e and y=log(1x)
View SolutionThe area between the curves y=lnxandy=(lnx)2 is
View SolutionFind the area enclosed by the graph of y=loge(x+1),y-axis, and the line y=1
View Solution
