The area bounded by y=x2,y=[x+1],0≤x≤2 and the y-axis is where [.] is greatest integer function.
A
13
B
√23
C
1
D
73
Video Solution
Text Solution
The correct Answer is:B
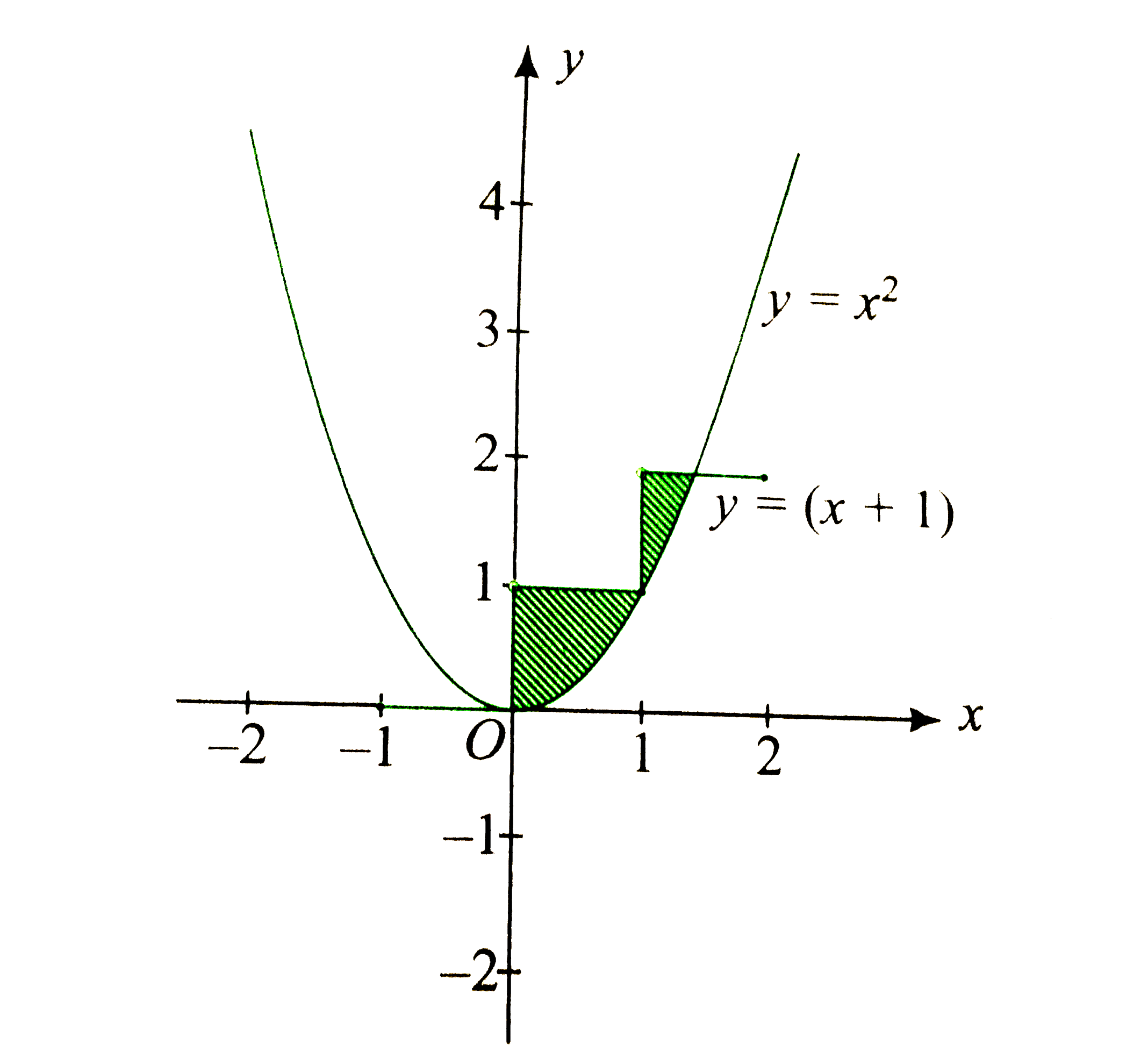
Area 1∫0(1−x2)dx+√2∫1(1−x2)dx=[x−x33]10+[x−x33]√21
=√23
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Multiple)
Explore 10 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Comprehension)
Explore 21 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.3
Explore 7 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
The area bounded by y=x2,y=√x,0≤x≤4 is
A203B103C10D503The area of region between y=4−x2,0≤x≤2 and the x-axis is
A43B73C163D53The area between y = x and y=x2,0≤x≤2 is
A1B23C13D43
Area of the region bounded by [x]2=[y]2 ,if x∈[1,3] (where [ .] denotes the greatest integer function),is less than
View SolutionThe area bounded by f(x)=x2,0≤x≤1,g(x)=−x+2,1≤x≤2 and x- axis is
View SolutionLet 'c' be a positive real number such that area bounded by y=0,y=[tan−1x] from x=0 to x=c is equal to area bounded by y=0,y=[cot−1x], from x=0 to x=c (where [⋆] represents greatest integer function), then
View SolutionThe area (in sq. units) bounded by [|x|]+[|y|]=2 in the first and third quardant is (where [.] is the greatest integer function).
View SolutionArea bounded by the curve y=logex,x=0,y≤0 and x-axis is:
View Solution
