The area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is

A

13+π24 sq. units

B

16+π38 sq. units

C

2 sq. units

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

y=sin−1|sinx|=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩x,0≤x<π2π−x,π2≤x<ππ−x,π≤x<3π22π−x,3π2≤x<2π
y=(sin−1|sinx|)2=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩x2,0≤x<π2(π−x)2,π2≤x<π(x−π)2,π≤x<3π2(2π−x)2,3π2≤x<2π
The required area A is shown as shaded region in the figure.
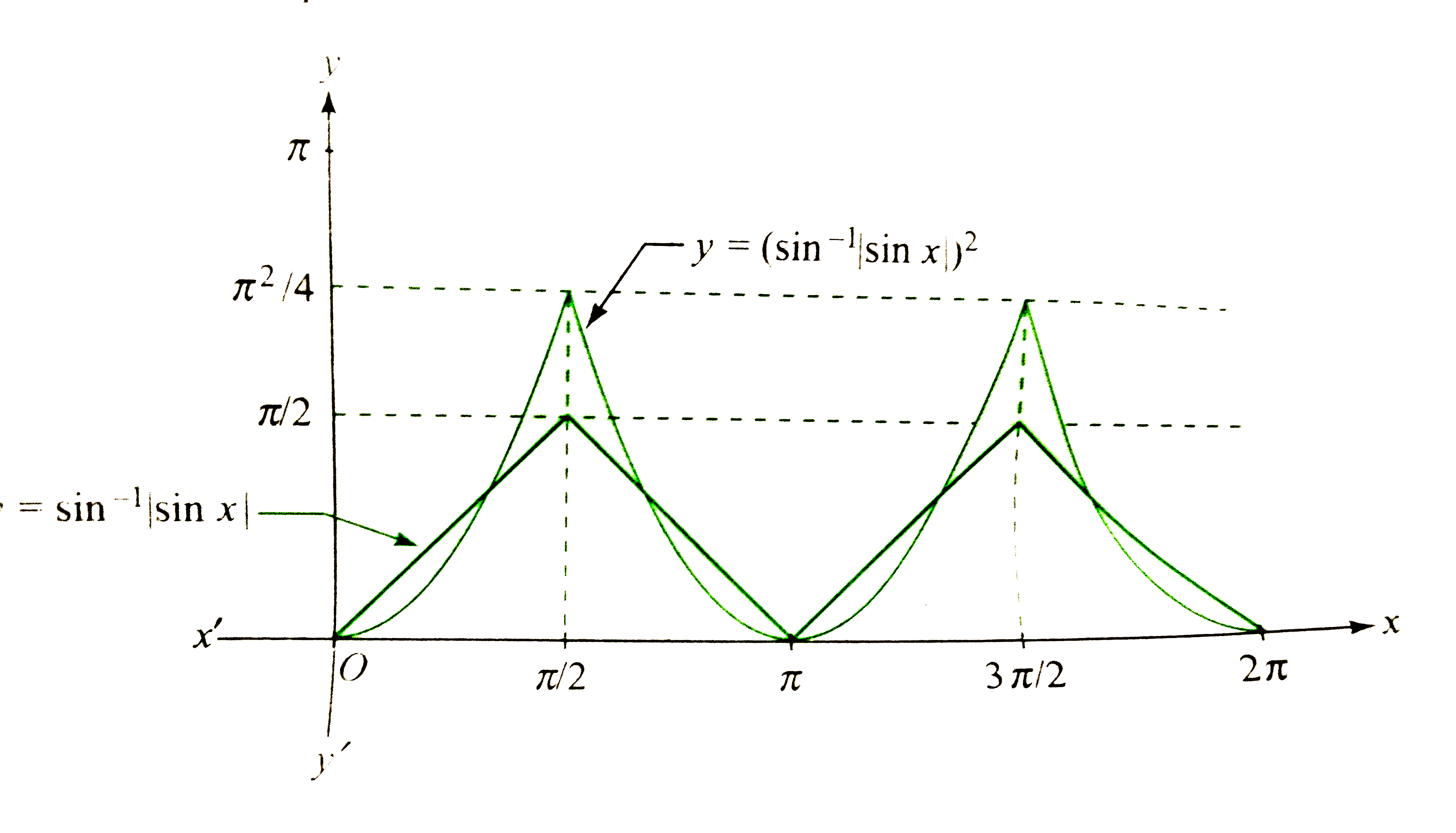
ocr_image
⇒ 41∫0(x−x1)dx+4π/2∫1(x2−x)dx
=43+π2[π−36] sq. units.

Updated on:21/07/2023
|
Class 12MATHSAPPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The area bounded by the curve y=sin2x, axis and y=1, is

    A1
    B1/4
    Cπ/4
    Dπ/4−1/2

  • The area bounded by the curves y=cos−1x,y=sin−1xandy=−πx3, where −1≤x≤1,is

    A3π2+1−√2 sq. units
    B3π4+1+√2 sq. units
    C3π4+2−√2 sq. units
    D3π4+1−√2 sq. units

  • Area bounded by the curves y=sin4x,x=0,x=π2 and y=0 is

    A3/8
    B3/16
    C3π/16
    DNone of these