Question

The area enclosed by the curves $x{y}^2=a^2(a-x)and(a-x)y^2=a^{2}x$ is

Options

A. `(pi-2)a^(2)` sq. units
B. `(4-pi)a^(2)` sq. units
C. `pia^(2)//3` sq. units
D. None of these

Answer

A

Explanation

The two curves are
`xy^(2)=a^(2)(a-x)or x=(a^(3))/(a^(2)+y^(2))" (1)"`
`"and "(a-x)y^(2)=a^(2)x`
`rArr" "x=(ay^(2))/(a^(2)+y^(2))=(ay^(2)+a^(3)-a^(3))/(a^(2)+y^(2))=a-(a^(3))/(a^(2)+y^(2))" (2)"`
Curve (1) is symmetrical about x-axis and have y-axis as the asympote.
Curve (2) is symmetrical about x-axis, tangent at origin as y-axis, and the asymptote x=a.
The two curves intersect at the point `P(a//2,a) and Q (a//2,-a).`

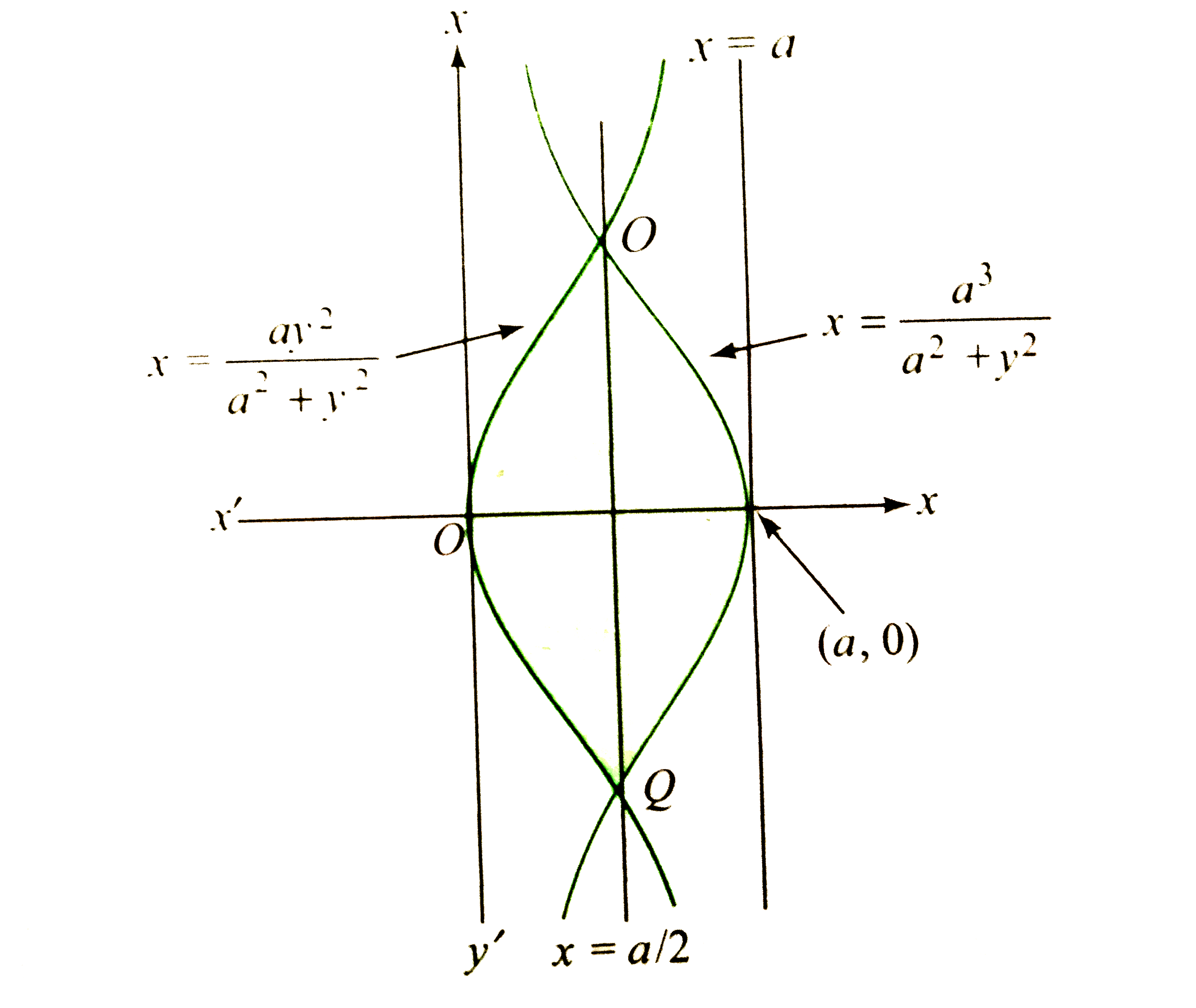
`"Required are "=2overset(a)underset(0)int[-a+(a^(3))/(a^(2)+y^(2))+(a^(3))/(a^(2)+y^(2))]dx`
(integrating along y-axis)
`=2[-ay+2a^(2)tan^(-1)""(y)/(a)]_(0)^(a)`
`=2[-a^(2)+2a^(2)(pi)/(4)]`
`=(pi,2)a^(2)` sq. units.