The area bounded by the curves y=xex,y=xe−x and the line x=1 is 2esq.units (b) 1−2esq.units 1esq.units (d) 1−1esq.units
2e sq. units
1−2e sq. units
1e sq. units
1−1e sq. units
The correct Answer is:A
Curve tracing : y=xex
Let dydx=0⇒ex+xex=0orx=−1.
Also, at x=−1,dydx changes sign from -ve to + ve,
Hence, x=-1 is a point of minima.
When x→∞,yrar∞
Also limx→−∞xex=limx→−∞xe−x=limx→−∞1e−x=0
With similar types of arguments, we can draw the graph of y=xe−x.
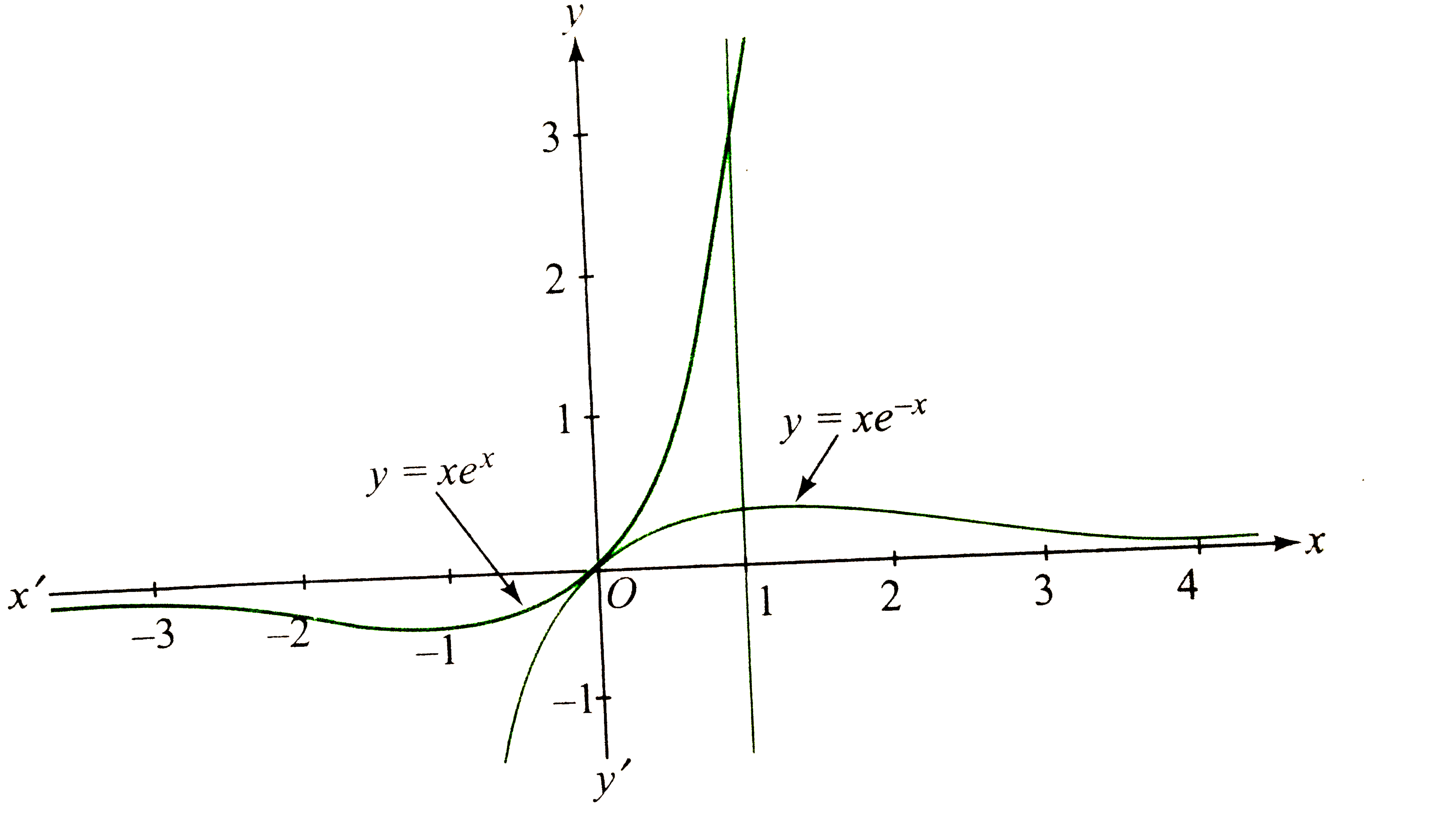
Required ara =∫10xexdx−∫10xe−xdx
=[xex]10−∫10exdx−([−xe−x]10+∫10e−xdx)
=e−(e−1)−(−e−1−(e−1−1))=2e sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
The area bounded by the two branches of curve (y−x)2=x3 and the straight line x=1 is 15sq.units (b) 35sq.units 45sq.units (d) 84sq.units
View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is 14sq.units (b) 43sq.units 54sq.units (d) 73sq.units
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
View SolutionLet f(x)=minimum(x+1,√1−x) for all x≤1. Then the area bounded by y=f(x) and the x-axis is
View SolutionConsider two curves C1:y2=4[√y]xandC2:x2=4[√x]y, where [.] denotes the greatest integer function. Then the area of region enclosed by these two curves within the square formed by the lines x=1,y=1,x=4,y=4 is 83sq.units (b) 103sq.units 113sq.units (d) 114sq.units
View SolutionThe area bounded by the curve f(x)=x+sinx and its inverse function between the ordinates x=0andx=2π is 4πsq.units (b) 8πsq.units 4sq.units (d) 8sq.units
View SolutionThe value of the parameter a such that the area bounded by y=a2x2+ax+1, coordinate axes, and the line x=1 attains its least value is equal to 14sq.units (b) 12sq.units 34sq.units (d) −1sq.units
View SolutionThe area bounded by the curve y2=8x and x2=8y is 163sq.units b. 316sq.units c. 143sq.units d. 314sq.units
View SolutionThe area of the region whose boundaries are defined by the curves y=2cosx,y=3tanx,andthey−aξsis 1+31n(2√3)sq.units 1+321n3−31n2sq.units 1+321n3−1n2sq.units 1n3−1n2sq.units
View Solution
