The area of the closed figure bounded by x=−1x=2, and y={−x2+2,x≤12x−1,x>1 and the abscissa axis is
A
16/3 sq. units
B
10/3 sq. units
C
13/3 sq. units
D
7/3 sq. units
Video Solution
Text Solution
The correct Answer is:A
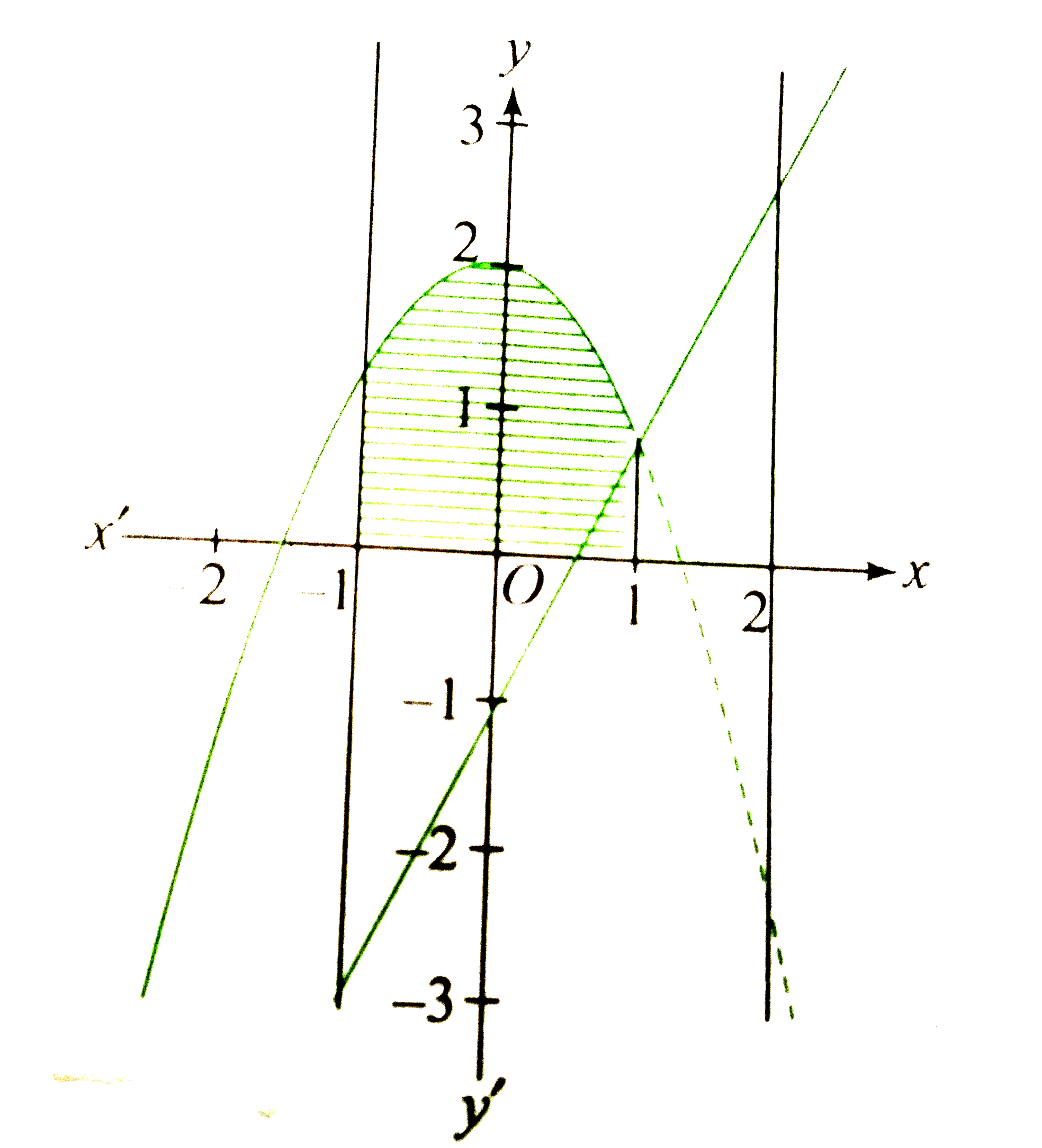
A=1∫−1(−x2+2)dx+2∫1(2x−1)dx
=(−x33+2x)1−1+(x2−x)21
=163 sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
The area (in square units) of the closed figure bounded by x=−1,x=2andy={−x2+2,x≤12x−1,x>1 and the abscissa axis, is
A16/3B13/3C13/3D7/3The area bounded by y=x2 and y=1−x2 is
A√8/3B16/3C32/3D16/3The area of the closed figure bounded by y=1/cos2x,x=0,y=0andx=π/4, is
Aπ/4B1+π/4C1D2
Find the area of the figure bounded by the parabolas x=−2y2,x=1−3y2.
View SolutionIf f(x)={2x2+1,x≤14x3−1,x>1, then ∫20f(x)dx is
View SolutionThe area of the closed figure bounded by x=−1,y=0,y=x2+x+1, and the tangent to the curve y=x2+x+1 at A(1,3) is
View SolutionThe area of the figure bounded by the curves y2=2x+1 and x−y−1=0 , is
View SolutionThe area of the closed figure bounded by the curves
y=cosx,y=1+2πxandx=π/2, is
View Solution
