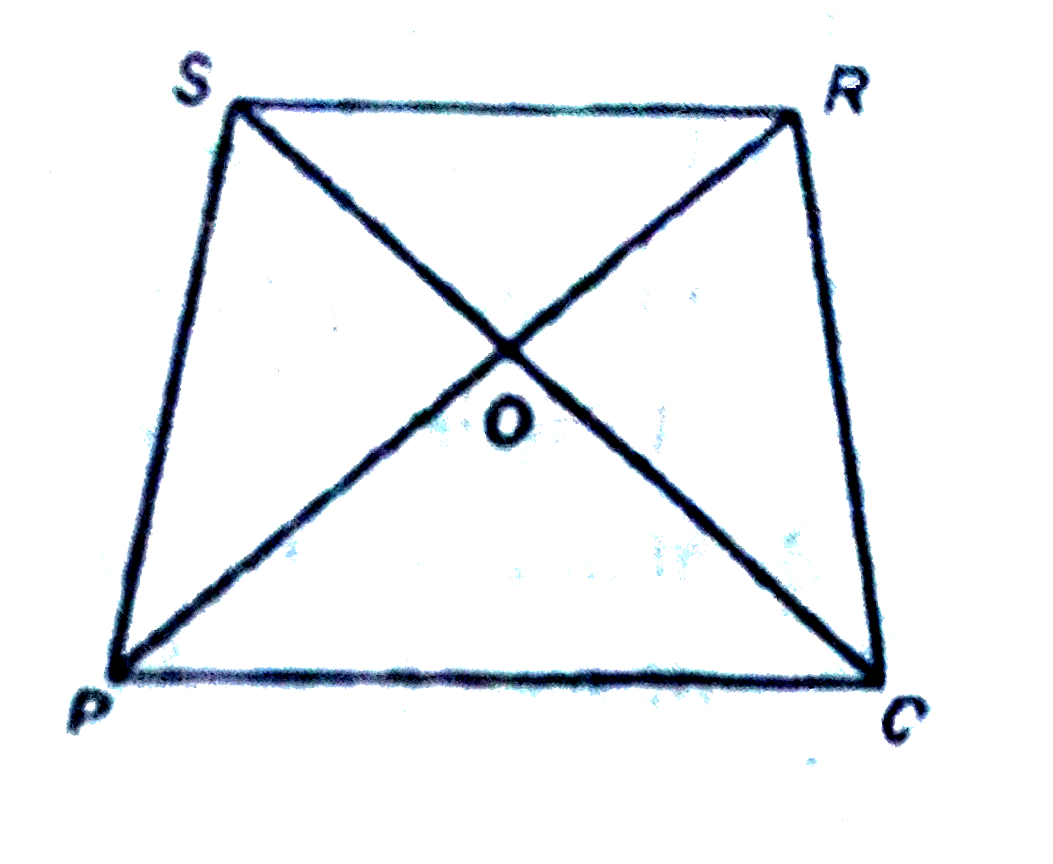
Diagonals of a trapezium PQRS intersect each other at the point 0 ,PQ||RS and PQ=3 RS. Find the ratio of the areas of ΔPOQ and ΔROS.
Video Solution
Text Solution
Here PQRS is a trapezium in which PQ||RS and PQ = 3RS. In △POQand△ROS
∠OPQ=∠ORS (alternate angles)
∠OQP=∠OSR (alternate angles)
△POQ~△ROS ( AA similarity)
area(△POQ)area(△ROS)=PQ2RS2
(3RS)2RS2=91=9:1
|
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
Diagonals of a Trapezium ΔBCD with AB || CD intersect each other at the point O. If AB = 2CD, then the ratio of the areas of ΔAOB and ΔCOD is
A4:1B1:16C1:4D16:1Diagonals of a quadrilateral PQRS bisect each other at right angles. If PQ = 5.5 cm, then the perimeter of PQRS is
A11cmB22cmC16.5cmD5.5(1+√2) cmABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C4:1D1:4
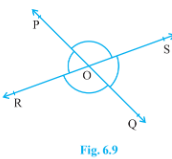
Lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionIn Fig: 6.9. lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7,find the all the angles..
View SolutionIn a trapezium ABCD, AB||DC and its digonals intersects at point O. AB = 6 cm, DC = 3 cm then find the ratio of area ΔAOBandΔCOD.
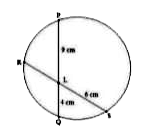
View SolutionIn the given figure, chords PQ and RS intersect each other at point L Find the length of RL.
View SolutionIn two isosceles ΔABC and ΔPQR, the ratio of sides AB : PQ is 1 : 3. Find the ratio of area of ΔABC and area of ΔPQR.
View Solution