In figure, if ∠1=∠2 and △NSQ≅△MTR, then prove that ΔPTS~ΔPRQ.
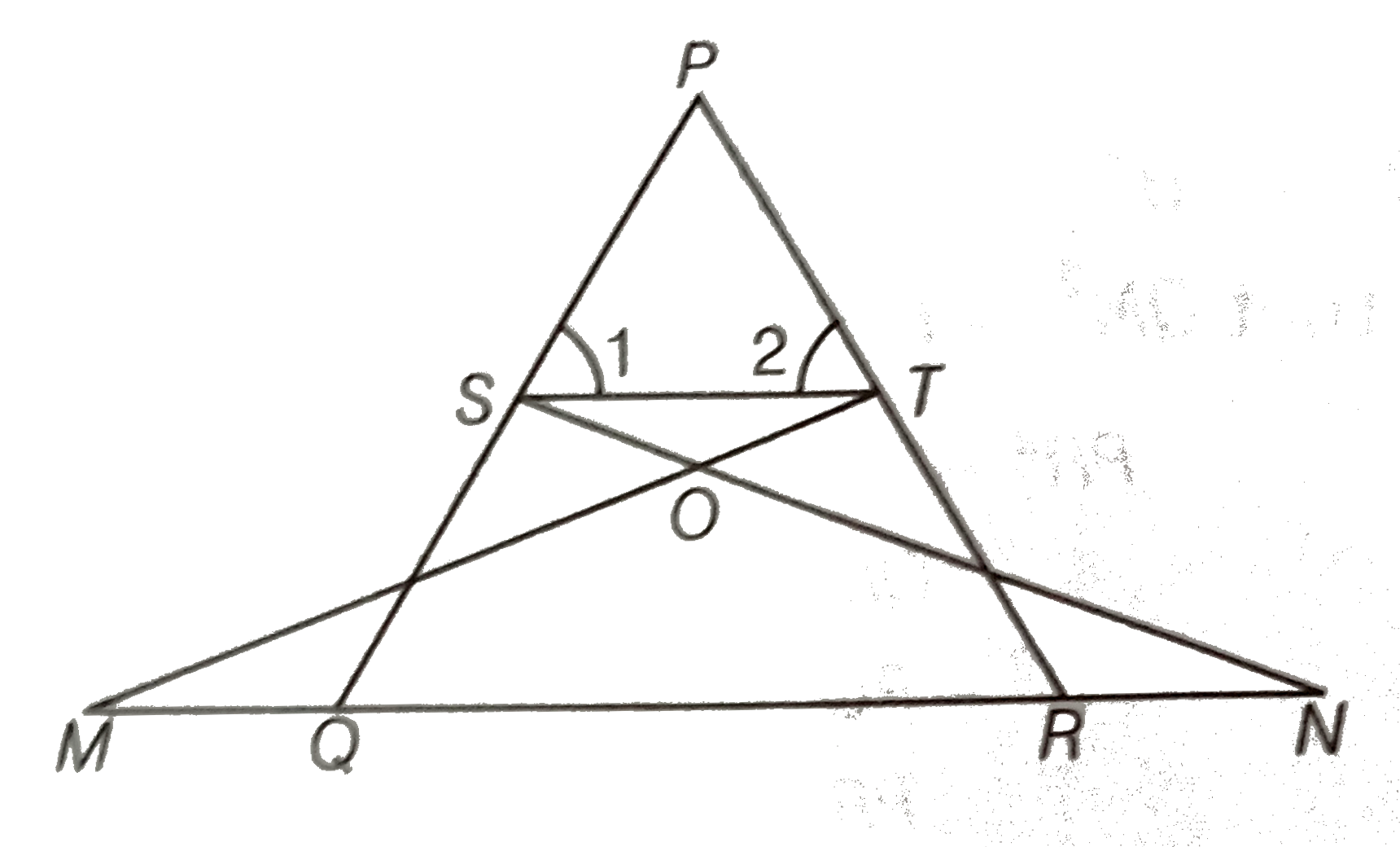
Given: In △PQR points S in on PQ and T is on PR.
such that ∠1=∠2
and △NSQ≅△MTR
To prove : △PTS~△PRQ
Proof : △NSQ≅△MTR ( given)
SQ = TR ( CPCT) ... (1)
∠1=∠2
PT = PS ( sides opposite to equal angles in △PTS) ...(2)
⇒ PTTR=PSSQ [ from (1), (2)]
ST||QR ( by converse of BPT)
Now in ,△PTSand△PRQ ,we have
ST||QR ( prove above)
∠1=∠3 (corresponding angles)
∠2=∠4 ( corresponding angles)
△PTS~△PRQ ( by AA similartiy criterion) Hence proved.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In the given figure, figure, if ∠1=∠2 and △NSQ≅△MTR, then prove that △PTS~△PRQ.
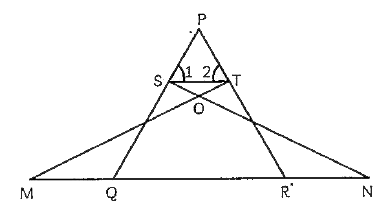
View SolutionIn figure, if ∠1=∠2 and ΔNSQ=ΔMTR, then prove that ΔPTS~ΔPRQ.
View SolutionIn figure, it is given that RT=TS,∠1=∠4and∠3=∠2. Prove that ΔRBT≅ΔSAT.
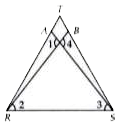
View SolutionIn the given figure ∠1=∠2 and ∠2=∠3
then show that ∠1=∠3

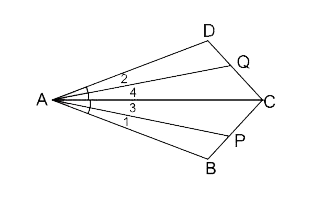
View SolutionIn the given figure , AB=AD , ∠1=∠2and∠3=∠4 .Prove that AP=AQ
View SolutionIn the given figure ∠1=∠3and∠2=∠4
then show that ∠BAD=∠BCD

View SolutionIn the adjoining figure, ∠BAC=∠BDC and ∠ABC=∠BCD. Prove that :
(i) ΔABC≅ΔDCB
(ii) ΔABE≅ΔDCF.

View SolutionIn the adjoining figure, we have ∠1=∠2 and ∠2=∠3. Show that ∠1=∠3.

View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
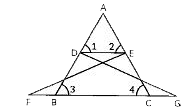
View SolutionIn the given figure, ΔFEC is congruent to ΔGDB and ∠1=∠2. Prove that ΔADE~ΔABC
View Solution

