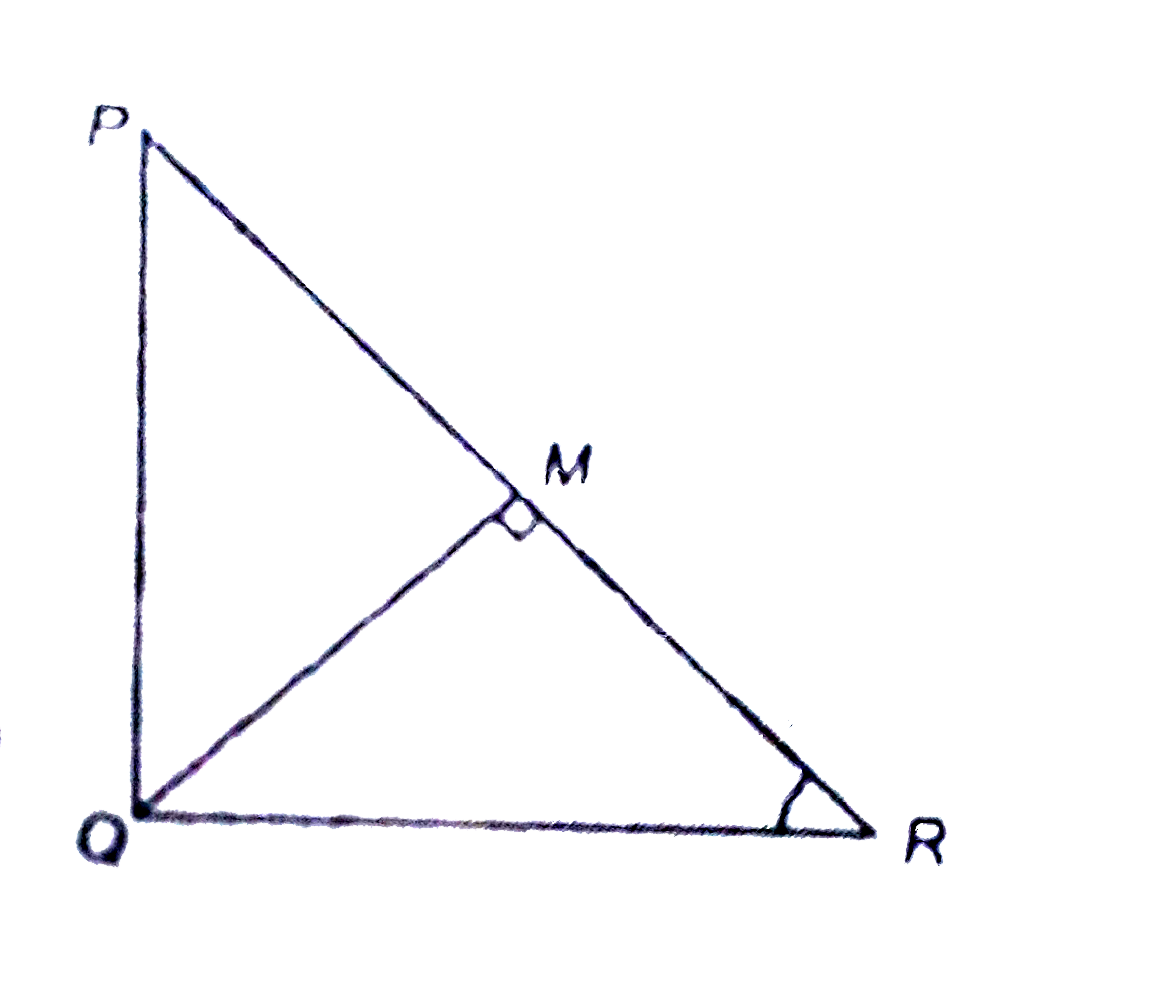
In PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
Video Solution
Text Solution
Given that
PR2−PQ2=QR2andQM⊥PR
PR2=PQ2+QR2
∠PQR=90∘ ( converse of Pythagoras theorem)
In △QMRand△PMQ
∠QMR=∠PMQ (each90∘))
∠MQR=∠MPQ (each90∘=∠R)
△QMR~∠PMQ (AA similarity)
⇒ area(△QMR)area(△PMQ)=QM2PM2
12×QM×RM12×QM×PM=QM2PM2
RM×PM=QM2
|
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
If P:Q:R=2:3:4 and P2+Q2+R2=11600,
then find (P+Q−R)A15B16C18D20If P : Q = 2 : 3 and P : R = 4 : 5, then what is (P + Q) : (Q + R)?
A20:27B20:17C10:11D20:29if P:Q:R=2:3:4andP2+Q2+R2=11600, then find P+Q+R, where P,Q and R are whole numbers.
A15B16C18D20
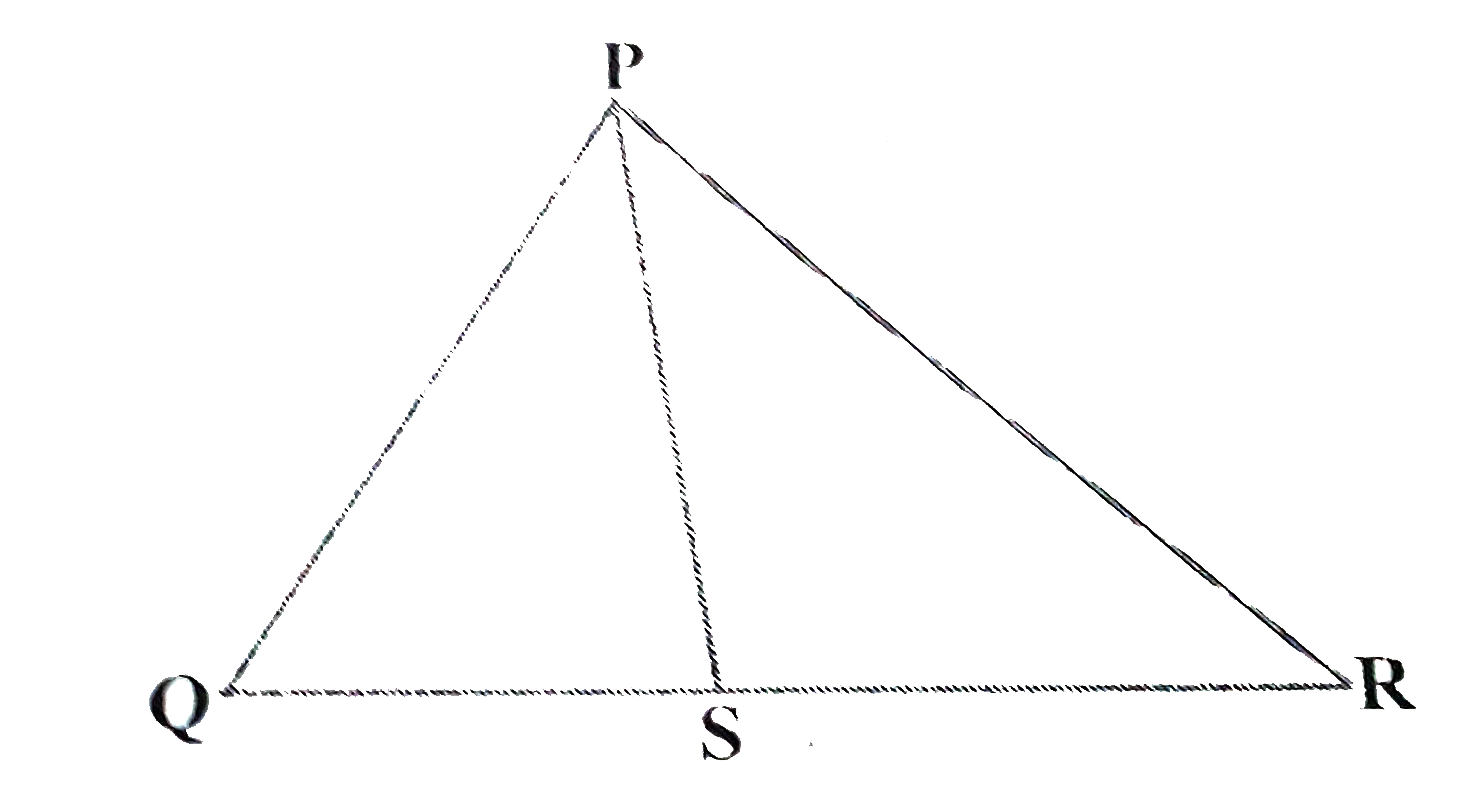
In figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
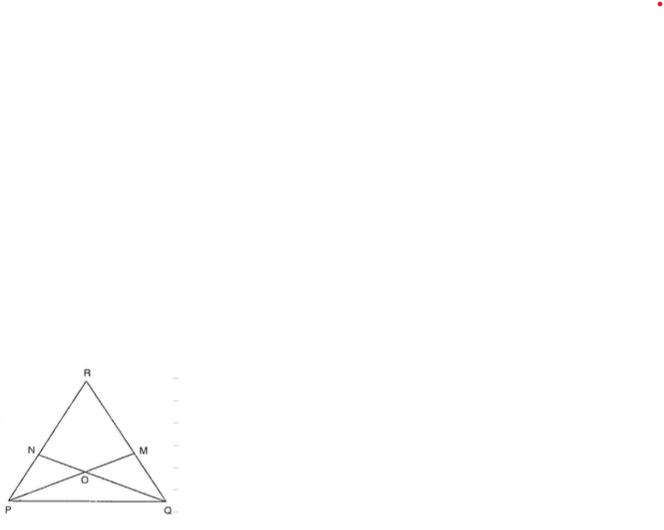
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View Solution


