ABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
Given: ABCD is a trapezium in which
AB||CD and
PQ ||DC (see figure)
Also, PD = 28 cm, BQ = 35 cm and QC = 15 cm
to find : AD
Proof: In trapezium ABCD,
AB || CD
PQ ||DC
AB||CD ||PQ …..(1)
in △BCD OQ||DC [ from (1)]
BOOD=BQQC ( by BPT) ...(2)
similarly , in △DAB
PO||AB
BOOD=APPD (by BPT ...(3)
from (2) and (3)
APPD=BQQC
⇒ AP28=3515
⇒AP=3525×18=7×6
AP=3515×18=7×6
AP = 42 cm
AD= AP +PD= 42 cm + 18 cm = 60 cm

Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
ABCD is a trapezium in which ABIIDC and P and Qare points on AD and BC respectively such that PQ||DC. If PD= 12 cm, BQ = 42 cm and QC = 18cm, find AD.
View SolutionABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
View Solution
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
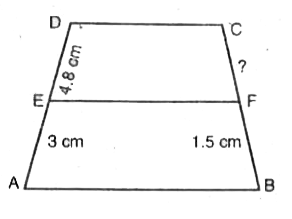 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseABCD is a trapezium of sides in which BC || AB & AB=9cm, BC=12cm, CD=15cm & DA=20cm. Find the sum of square of its diagonal.
A638B786C838D814In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
ABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about

View SolutionABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
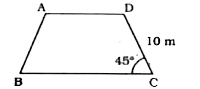
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about

View Solution

