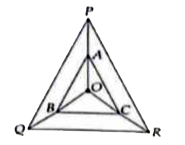
In figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
In figure AB||PQ (given )
⇒ OAAP=OBBQ
( basic proportonality theorem) ….(1)
Also in figure AC||PR (given)
⇒ OAAP=OCCR ( basic proportionality theorem) …. (2)
from equatlons ( 1) and (2) , we get
OBBQ=OCCR
BC||QR ( converse of basic proportionality theorem)

Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6a
Explore 23 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
Knowledge Check
In △PQR, M and N are points on PQ and PR, respectively, such that ¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯QR, If PM =x, PR =x+9,PQ=x+13 and PN=x−2, then find x.
A10B11C13D15In triangle PQR, points A,B, and C are taken on PQ, PR and QR respectively such that QC=AC and CR=CB . If ∠QPR=40∘ then ∠ACB is equal to :
A140∘B40∘C70∘D100∘
In the given figure points A, B, C respectively lie on sides OP, OQ such that AB||PQandAC||PR show that BC∣∣QR
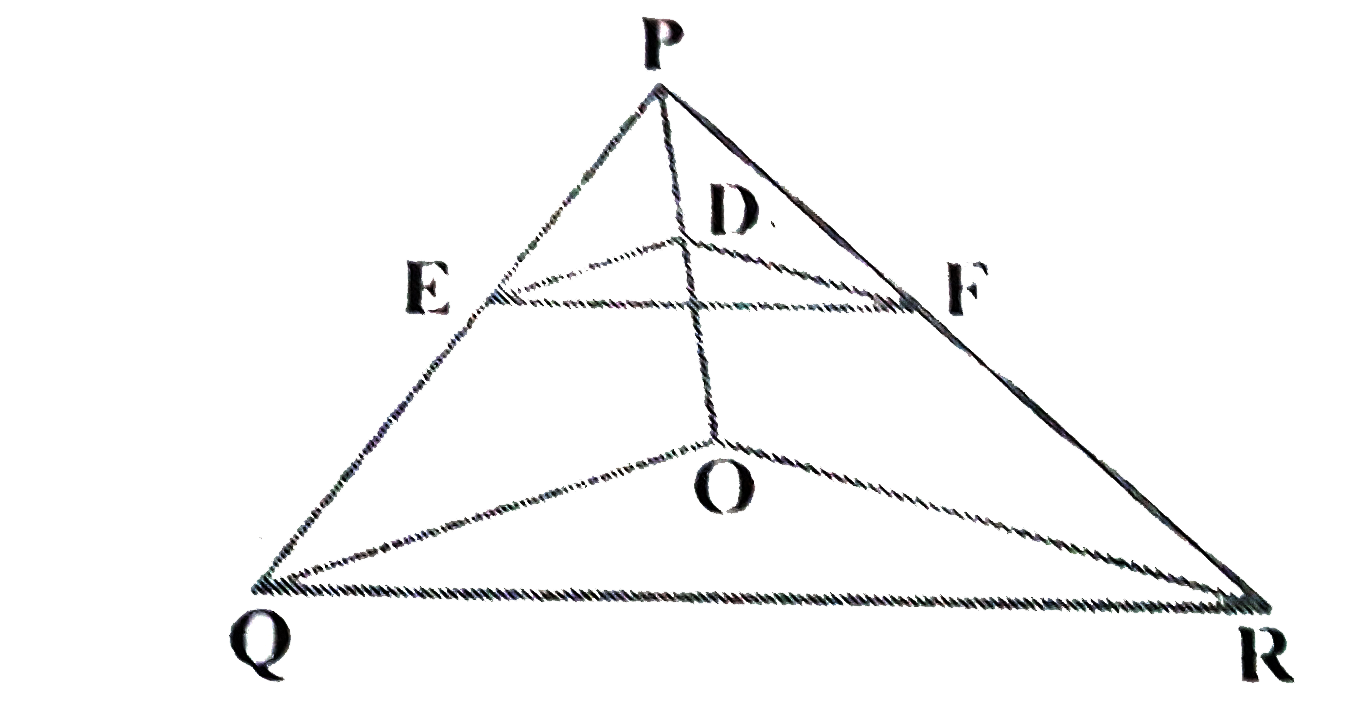
View SolutionIn figure DE || OQ and DF || OR. Show that EF||QR.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
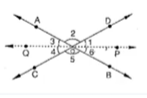
View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View Solution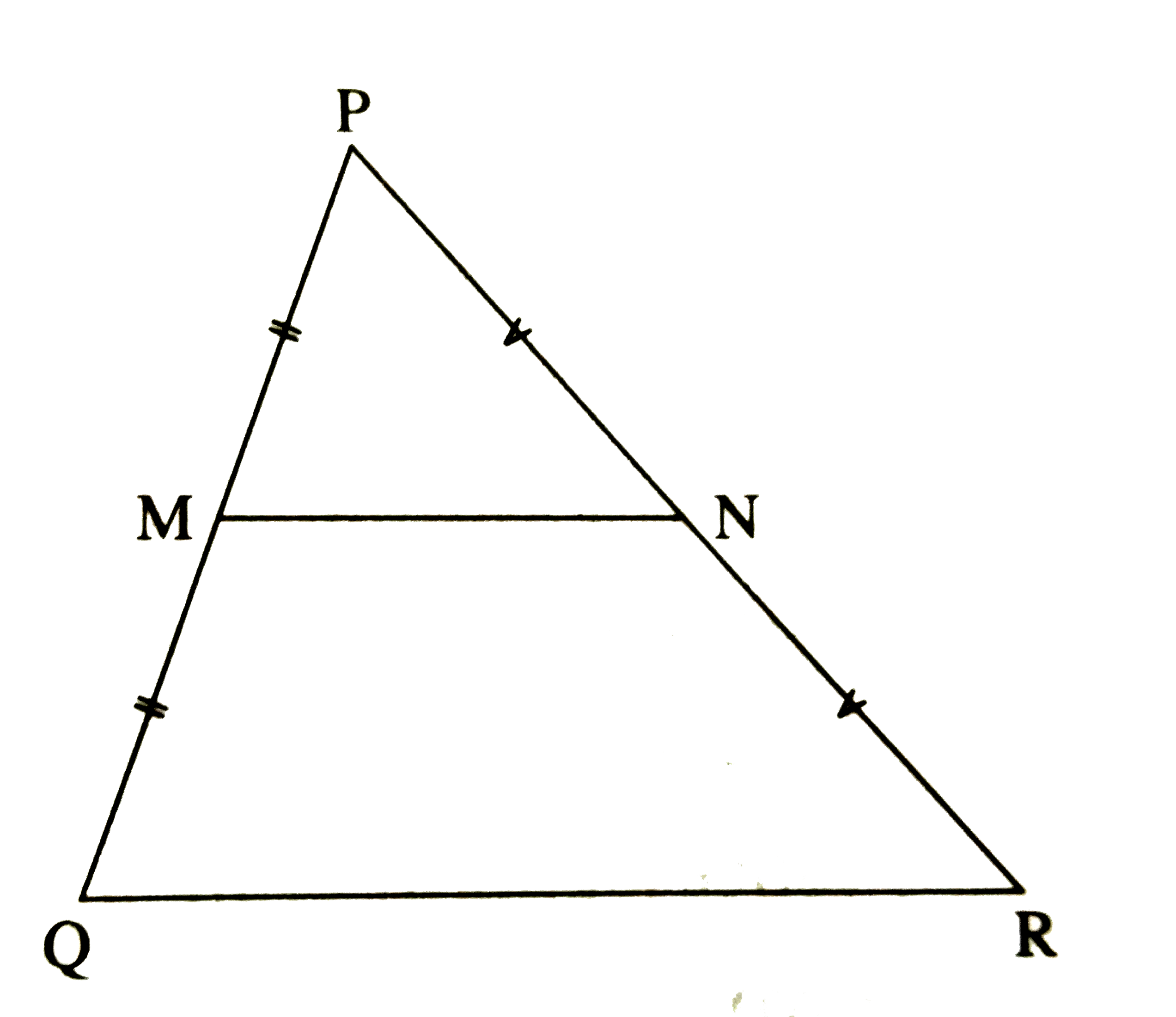
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View Solution


