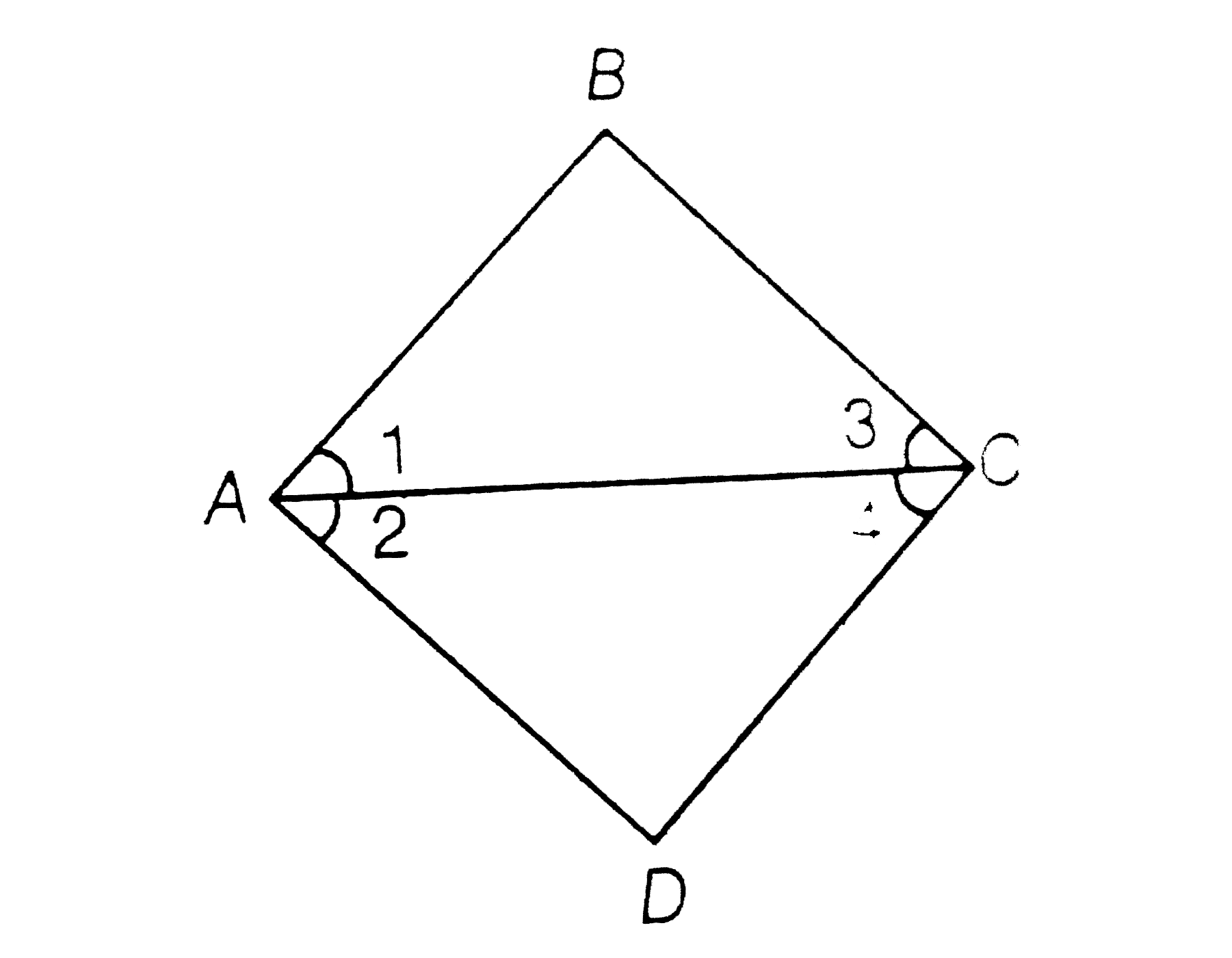
In the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
To prove that angle A is equal to angle C given that angle 1 = angle 3 and angle 2 = angle 4, we can follow these steps:
1. Identify the Given Information:
We are given that:
- Angle 1 = Angle 3
- Angle 2 = Angle 4
2. Apply the Axiom:
According to the second axiom of equality, if equal quantities are added to equal quantities, the sums are equal. We will apply this axiom here.
3. Add the Angles:
We add angle 1 and angle 2, and angle 3 and angle 4:
Angle 1+Angle 2=Angle 3+Angle 4
4. Substitute the Equal Angles:
Substitute the values from the given information:
Angle 1+Angle 2=Angle 3+Angle 4
becomes:
Angle 3+Angle 2=Angle 3+Angle 4
5. Simplify the Equation:
Since angle 3 is common on both sides of the equation, we can subtract angle 3 from both sides:
Angle 2=Angle 4
6. Conclude the Proof:
Since we know that:
Angle A=Angle 1+Angle 2
and
Angle C=Angle 3+Angle 4
and substituting the equal angles, we find:
Angle A=Angle C
Thus, we have shown that angle A is equal to angle C.
We are given that:
- Angle 1 = Angle 3
- Angle 2 = Angle 4
According to the second axiom of equality, if equal quantities are added to equal quantities, the sums are equal. We will apply this axiom here.
We add angle 1 and angle 2, and angle 3 and angle 4:
Angle 1+Angle 2=Angle 3+Angle 4
Substitute the values from the given information:
Angle 1+Angle 2=Angle 3+Angle 4
becomes:
Angle 3+Angle 2=Angle 3+Angle 4
Since angle 3 is common on both sides of the equation, we can subtract angle 3 from both sides:
Angle 2=Angle 4
Since we know that:
Angle A=Angle 1+Angle 2
and
Angle C=Angle 3+Angle 4
and substituting the equal angles, we find:
Angle A=Angle C
Topper's Solved these Questions
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - RS AGGARWALCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Example
1 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - RS AGGARWALCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
6 Videos
- GEOMETRICAL CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - GEOMETRICAL CONSTRUCTIONSEXERCISE - Exercise 13
2 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
Similar Questions
In the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
View SolutionIn the given figure ∠1=∠3and∠2=∠4
then show that ∠BAD=∠BCD

View SolutionIn the adjoining figure, we have ∠1=∠2 and ∠2=∠3. Show that ∠1=∠3.

View SolutionIn the given figure ∠1=∠2 and ∠2=∠3
then show that ∠1=∠3

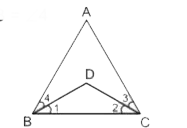
View SolutionIn given figure ∠ABC=∠ACBand∠3=∠4
Show that ∠1=∠2
View SolutionIn the given figure we have ∠1=∠3,∠2=∠4and∠3=∠4 prove that ∠1=∠2
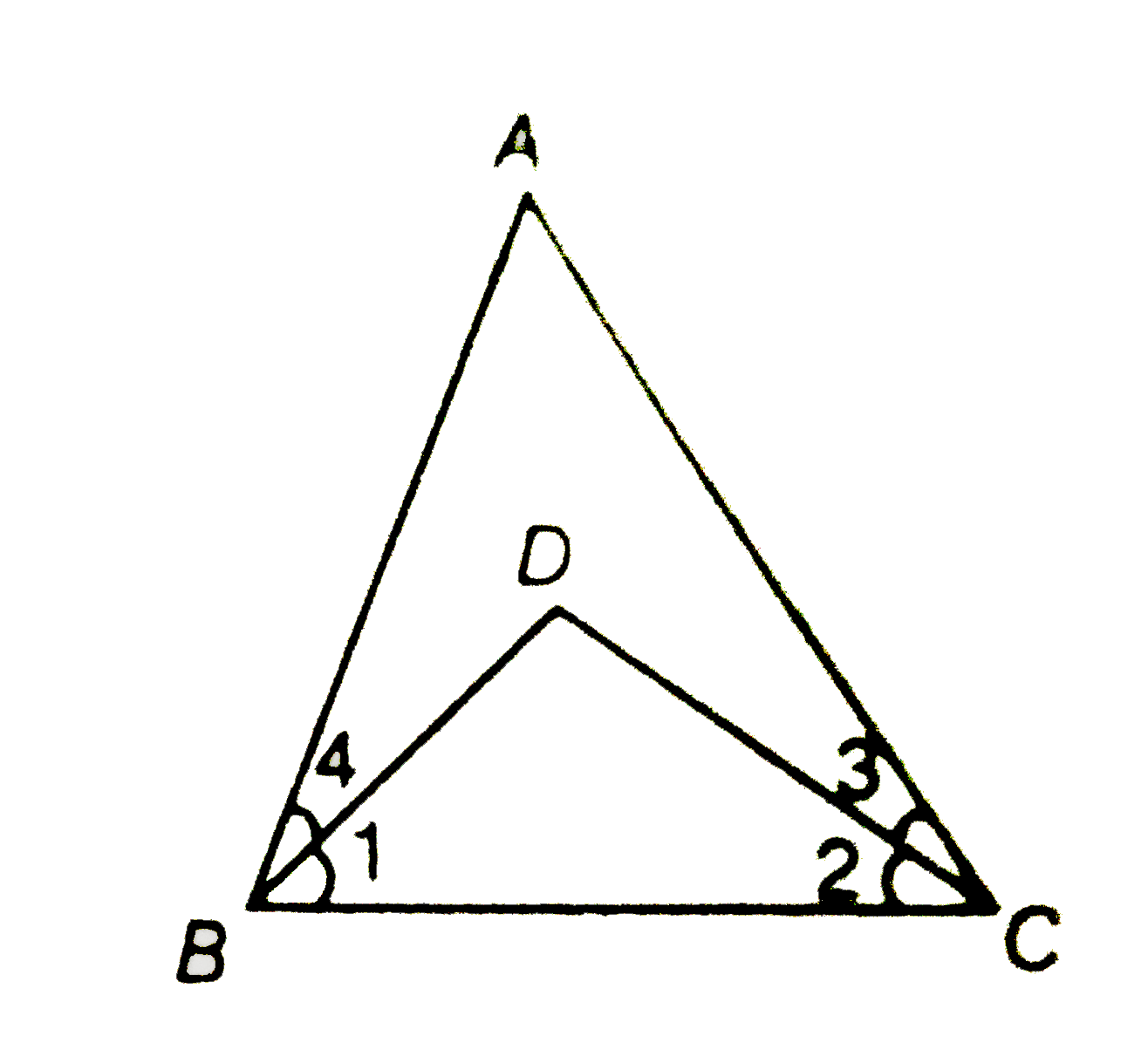
View SolutionIn the ajoining figure , we have∠ABC=∠ACBand∠3=∠4. Show that BD=DC.
View SolutionIn the given figure, name the angles indicated as

∠2
View SolutionIn the given figure, name the angles indicated as

∠12
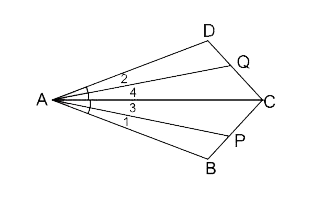
View SolutionIn the given figure , AB=AD , ∠1=∠2and∠3=∠4 .Prove that AP=AQ
View Solution
