Lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
1. Understand the Problem:
We have two lines, PQ and RS, that intersect at point O. We are given the ratio of angles ∠POR to ∠ROQ as 5:7.
2. Assign Variables to Angles:
Let ∠POR=5x and ∠ROQ=7x for some variable x.
3. Use the Straight Line Property:
Since angles POR and ROQ are on the same straight line, we can write:
∠POR+∠ROQ=180∘
Substituting the expressions for the angles, we have:
5x+7x=180∘
4. Combine Like Terms:
Combine the terms on the left:
12x=180∘
5. Solve for x:
Divide both sides by 12:
x=180∘12=15∘
6. Find the Angles:
Now substitute x back to find ∠POR and ∠ROQ:
- ∠POR=5x=5×15∘=75∘
- ∠ROQ=7x=7×15∘=105∘
7. Identify Vertically Opposite Angles:
Since ∠POR and ∠SOQ are vertically opposite angles, we have:
∠SOQ=∠POR=75∘
Similarly, ∠POS and ∠ROQ are also vertically opposite:
∠POS=∠ROQ=105∘
Summary of Angles:
- ∠POR=75∘
- ∠ROQ=105∘
- ∠SOQ=75∘ (vertically opposite to ∠POR)
- ∠POS=105∘ (vertically opposite to ∠ROQ)
Final Angles:
- ∠POR=75∘
- ∠ROQ=105∘
- ∠SOQ=75∘
- ∠POS=105∘
We have two lines, PQ and RS, that intersect at point O. We are given the ratio of angles ∠POR to ∠ROQ as 5:7.
Let ∠POR=5x and ∠ROQ=7x for some variable x.
Since angles POR and ROQ are on the same straight line, we can write:
∠POR+∠ROQ=180∘
Substituting the expressions for the angles, we have:
5x+7x=180∘
Combine the terms on the left:
12x=180∘
Divide both sides by 12:
x=180∘12=15∘
Now substitute x back to find ∠POR and ∠ROQ:
- ∠POR=5x=5×15∘=75∘
- ∠ROQ=7x=7×15∘=105∘
Since ∠POR and ∠SOQ are vertically opposite angles, we have:
∠SOQ=∠POR=75∘
Similarly, ∠POS and ∠ROQ are also vertically opposite:
∠POS=∠ROQ=105∘
- ∠POR=75∘
- ∠ROQ=105∘
- ∠SOQ=75∘ (vertically opposite to ∠POR)
- ∠POS=105∘ (vertically opposite to ∠ROQ)
- ∠POR=75∘
- ∠ROQ=105∘
- ∠SOQ=75∘
- ∠POS=105∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S, then PQRS is a
ArectangleBrhombusCparallelogramDquadrilateral whose opposite angles are supplementaryP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘
In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

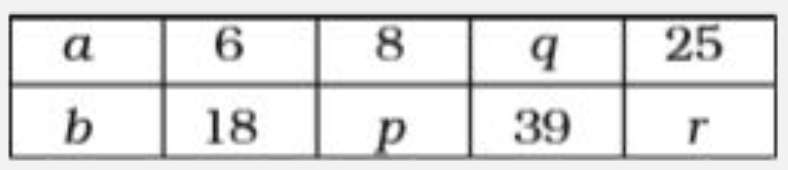
View SolutionIf a and b vary inversely to each other, then find the values of p, q, r .
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionWhen two forces of magnitude P and Q are perpendicular to each other, their resultant is of magnitude R. When they are at an angle of 180∘ to each other their resultant is of magnitude R√2 . Find the ratio of P and Q.
View Solution
