In two isosceles ΔABC and ΔPQR, the ratio of sides AB : PQ is 1 : 3. Find the ratio of area of ΔABC and area of ΔPQR.
A)1:3
B)1:9
C)9:1
D)3:1
The correct Answer is:B
To solve the problem of finding the ratio of the areas of two isosceles triangles, ΔABC and ΔPQR, given the ratio of their corresponding sides, we can follow these steps:
Step 1: Understand the Given Information
We know that the ratio of the sides AB to PQ is given as:
AB:PQ=1:3
Step 2: Identify the Corresponding Sides
Since both triangles are isosceles, we can also assume that:
- AC (the other equal side of ΔABC) is also equal to AB
- PR (the other equal side of ΔPQR) is equal to PQ
Thus, we have:
AC:PR=1:3
Step 3: Establish the Ratio of the Sides
From the information provided, we can denote:
- Let AB=1x
- Let PQ=3x
Step 4: Use the Area Ratio Formula
The area of similar triangles is proportional to the square of the ratio of their corresponding sides. Therefore, if the ratio of the sides is a:b, then the ratio of the areas will be:
Area ratio=(ab)2
Step 5: Calculate the Area Ratio
Substituting the values we have:
Area ratio=(13)2=1232=19
Conclusion
Thus, the ratio of the area of ΔABC to the area of ΔPQR is:
Area of ΔABC:Area of ΔPQR=1:9
Final Answer
The ratio of the area of ΔABC to the area of ΔPQR is 1:9.
---
We know that the ratio of the sides AB to PQ is given as:
AB:PQ=1:3
Since both triangles are isosceles, we can also assume that:
- AC (the other equal side of ΔABC) is also equal to AB
- PR (the other equal side of ΔPQR) is equal to PQ
AC:PR=1:3
From the information provided, we can denote:
- Let AB=1x
- Let PQ=3x
The area of similar triangles is proportional to the square of the ratio of their corresponding sides. Therefore, if the ratio of the sides is a:b, then the ratio of the areas will be:
Area ratio=(ab)2
Substituting the values we have:
Area ratio=(13)2=1232=19
Thus, the ratio of the area of ΔABC to the area of ΔPQR is:
Area of ΔABC:Area of ΔPQR=1:9
The ratio of the area of ΔABC to the area of ΔPQR is 1:9.
Similar Questions
Knowledge Check
ΔABCandΔPQR are congruent if _______
AAB=BC=AC and PQ=QR=PRB∠A=∠P,∠B=∠Qand∠C=∠RCAB=PQ,BC=QRand∠B=∠QDAB=PR,BC=RTand∠C=∠TIf ΔABC−ΔDEF such that AB = 1.2 cm and DE= 1.4 cm, the ratio of the areas of ΔABC and ΔDEF is:
A49:36B6:7C7:6D36:49If ABCD is a trapezium with AB || DC then which of the following is ratio of area of ΔABC and area of ΔBCD.
AAB:CDBCD:ABCAD:BCDBC:AD
In ΔABC PQ||BC. P and Q lies on side AB and AC respectively. If AB = 3AP, then what is the ratio of areas of ΔAPQandΔABC?
View SolutionIn ΔABC line PQ is drawn parallel to side BC where P and Q are respectively lie on side AB and AC. If AB = 3AP, what is the ratio of area of ΔAPQ to area of ΔABC ?
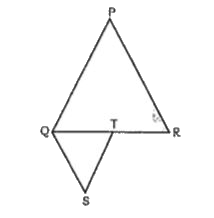
View SolutionΔPQR and ΔQST are two equilateral triangles such that T is the mid-point of QR. Find the ratio of the areas of ΔPQR and ΔQST.
View SolutionIn ΔABC, the medians AD and BE meet at G. The ratio of the areas of ΔBDG and the quadrilateral GDCE is :
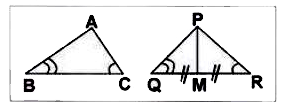
View SolutionIn ΔABC and ΔPQR,∠B=∠Q,∠C=∠R. M is the midpoint on QR.If AB:PQ=7:4, then
area(ΔABC)area(ΔPMR) is
View Solution
