A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as

A

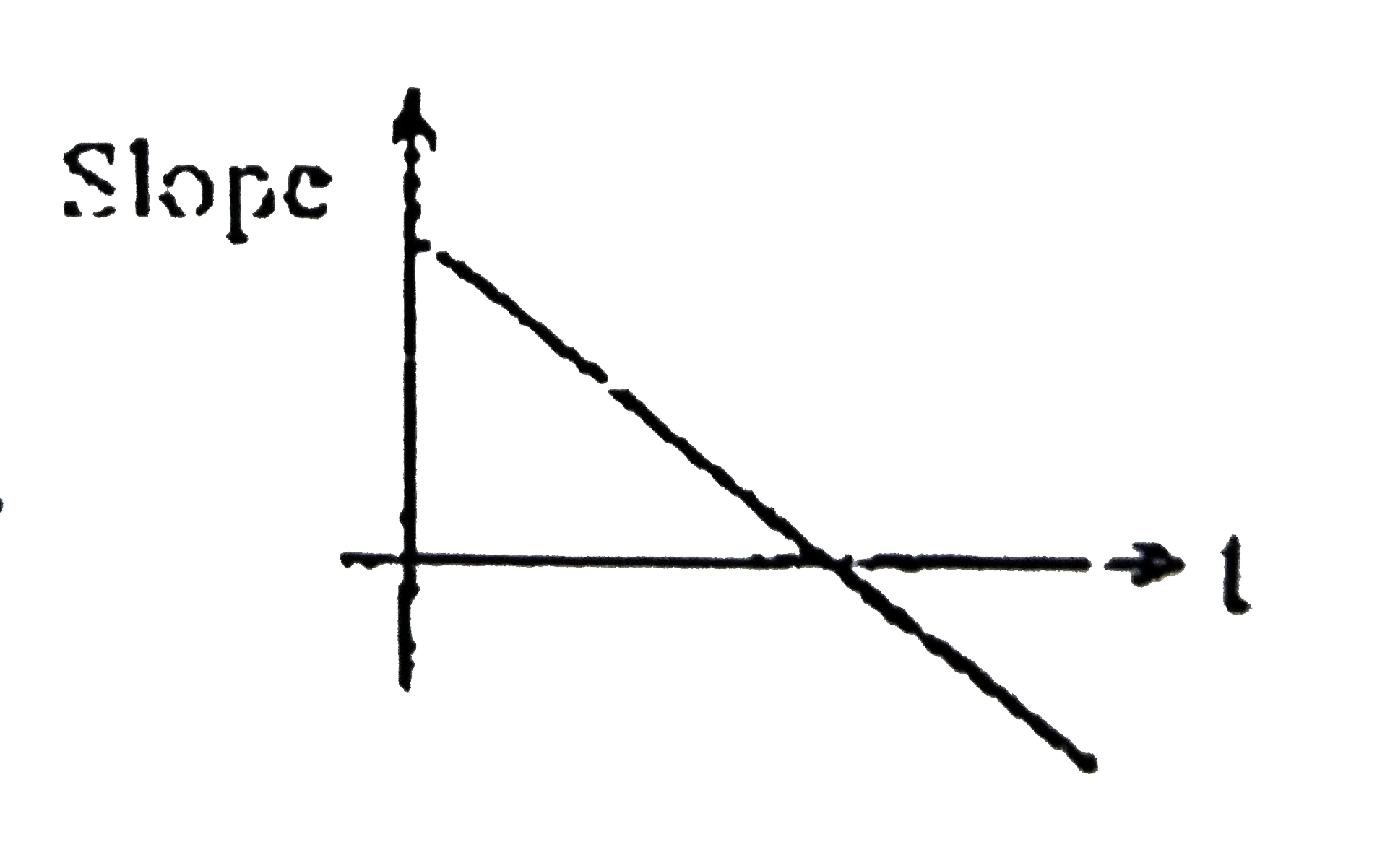
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

$y = x tan θ - \frac{g x^{2}}{2 u^{2} {cos}^{2} θ}$
$\Rightarrow \frac{d y}{d x} = tan θ - (\frac{g}{u^{2} {cos}^{2} θ}) x$
Putting x= $u cos θ . t$
$\Rightarrow \frac{d y}{d x} = tan θ - (\frac{g}{u cos θ}) t$
$\Rightarrow e q^{n}$ of straght line with negative slope and +ve intercept.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A
B
C
D
Question 2 - Select One
A particle is projected with a velocity $u$ making an angle $θ$ with the horizontal. The instantaneous power of the gravitational force
A(a) Varies linearly with time
B(b) Is constant throughout
C(c) Is negative for complete path
D(d) None of the above
Question 3 - Select One
A particle is projeced with a velocity $u$ making an angle $θ$ with the horizontal. The instantaneous power of the gravitational force
Avaries linearly with time
Bis constant throughout the path
Cis negative for complete path
Dvaries inversly with time

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile