A particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time .
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the initial conditions
The particle has a mass m, charge q, and is projected with a velocity v at an angle θ with respect to a uniform magnetic field B. The magnetic field is assumed to be along the z-axis (or k-direction).
Step 2: Resolve the initial velocity
The initial velocity →v can be resolved into two components:
- The component parallel to the magnetic field (along the z-axis):
vz=vcosθ
- The component perpendicular to the magnetic field (in the y-direction):
vy=vsinθ
Thus, the initial velocity vector can be expressed as:
→v0=vsinθ^j+vcosθ^k
Step 3: Analyze the motion in the magnetic field
In a magnetic field, the force on a charged particle is given by the Lorentz force:
→F=q(→v×→B)
Since the magnetic field is along the z-axis, the force will act in the x- and y-directions, causing circular motion in the plane perpendicular to the magnetic field.
Step 4: Determine the time of motion
The time given in the problem is:
t=πm2qB
This time corresponds to a quarter of the period of revolution of the particle in the magnetic field.
Step 5: Find the final velocity after time t
After a time t, the particle will have rotated 90∘ in the plane perpendicular to the magnetic field. The z-component of the velocity remains unchanged:
vz=vcosθ
The y-component of the velocity will change direction:
v′y=−vsinθ
Thus, the final velocity vector after time t is:
→vf=−vsinθ^i+vcosθ^k
Step 6: Calculate the change in velocity
The change in velocity Δ→v is given by:
Δ→v=→vf−→v0
Substituting the values:
Δ→v=(−vsinθ^i+vcosθ^k)−(vsinθ^j+vcosθ^k)
This simplifies to:
Δ→v=−vsinθ^i−vsinθ^j
Step 7: Calculate the magnitude of the change in velocity
The magnitude of the change in velocity is:
|Δ→v|=√(−vsinθ)2+(−vsinθ)2=√2(vsinθ)2=vsinθ√2
Final Answer
The magnitude of the change in velocity of the particle after time t is:
|Δ→v|=v√2sinθ
The particle has a mass m, charge q, and is projected with a velocity v at an angle θ with respect to a uniform magnetic field B. The magnetic field is assumed to be along the z-axis (or k-direction).
The initial velocity →v can be resolved into two components:
- The component parallel to the magnetic field (along the z-axis):
vz=vcosθ
- The component perpendicular to the magnetic field (in the y-direction):
vy=vsinθ
Thus, the initial velocity vector can be expressed as:
→v0=vsinθ^j+vcosθ^k
In a magnetic field, the force on a charged particle is given by the Lorentz force:
→F=q(→v×→B)
Since the magnetic field is along the z-axis, the force will act in the x- and y-directions, causing circular motion in the plane perpendicular to the magnetic field.
The time given in the problem is:
t=πm2qB
This time corresponds to a quarter of the period of revolution of the particle in the magnetic field.
After a time t, the particle will have rotated 90∘ in the plane perpendicular to the magnetic field. The z-component of the velocity remains unchanged:
vz=vcosθ
The y-component of the velocity will change direction:
v′y=−vsinθ
Thus, the final velocity vector after time t is:
→vf=−vsinθ^i+vcosθ^k
The change in velocity Δ→v is given by:
Δ→v=→vf−→v0
Substituting the values:
Δ→v=(−vsinθ^i+vcosθ^k)−(vsinθ^j+vcosθ^k)
This simplifies to:
Δ→v=−vsinθ^i−vsinθ^j
The magnitude of the change in velocity is:
|Δ→v|=√(−vsinθ)2+(−vsinθ)2=√2(vsinθ)2=vsinθ√2
The magnitude of the change in velocity of the particle after time t is:
|Δ→v|=v√2sinθ
Topper's Solved these Questions
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-2
13 Videos
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-3
4 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
- NUCLEAR PHYSICSBOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions
54 Videos
Similar Questions
A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View Solution
Knowledge Check
A particle of mass m is projected with velocity making an angle of 45∘ with the horizontal When the particle lands on the level ground the magnitude of the change in its momentum will be .
A√2mvBZeroC2 mvDmv√2A charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqBA charged particle enters into a magnetic field with velocity vector making an angle of 30∘ with respect of the direction of magnetic field. The path of the particle is
AcircularBhelicalCellipticalDstraight line
A particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionA proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
View SolutionA plane metallic sheet is placed with its face parallel to lines of magnetic induction B of a uniform field. A particle of mass m and charge q is projected with a velocity v from a distance d from the plane normal to the lines of induction. Then, the maximum velocity of projection for which the particle does not hit the plate is
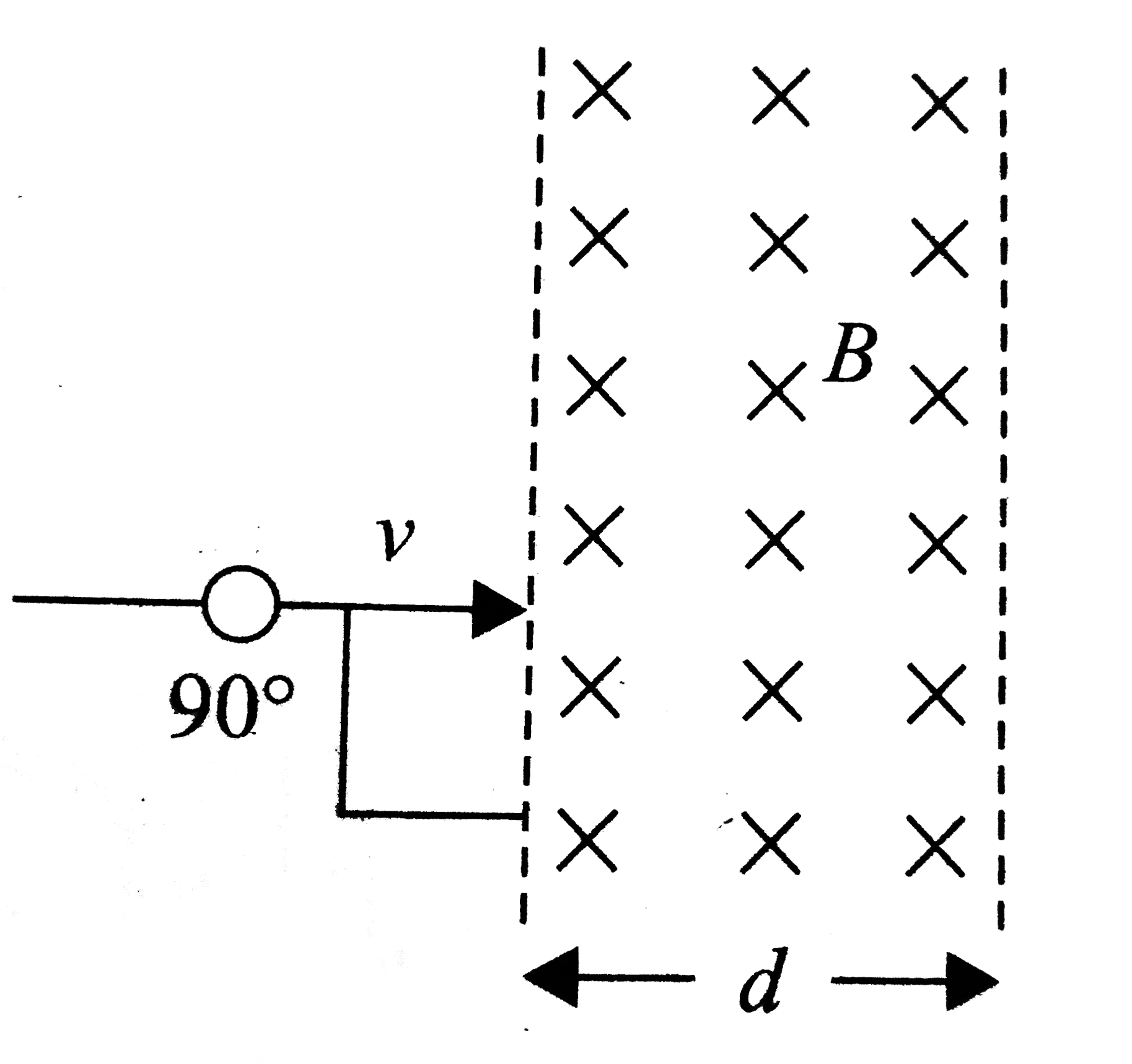
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
View SolutionA charge particle moves with velocity →V in a uniform magnetic field →B . The magnetic force experienced by the particle is
View Solution
