A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
Radius of the circular path R=mvqB
Angular velocity of the particle ω=vR=qBm
The speed of the particle will remain unchanged. The centre of circular path will be located on z-axis at point C. Let us take time interval t. during this time interval the particle will rotate an angel θ=ωt=qBtm.
Let us draw the front view of the circular path and locate the instantaneous position of the particle.
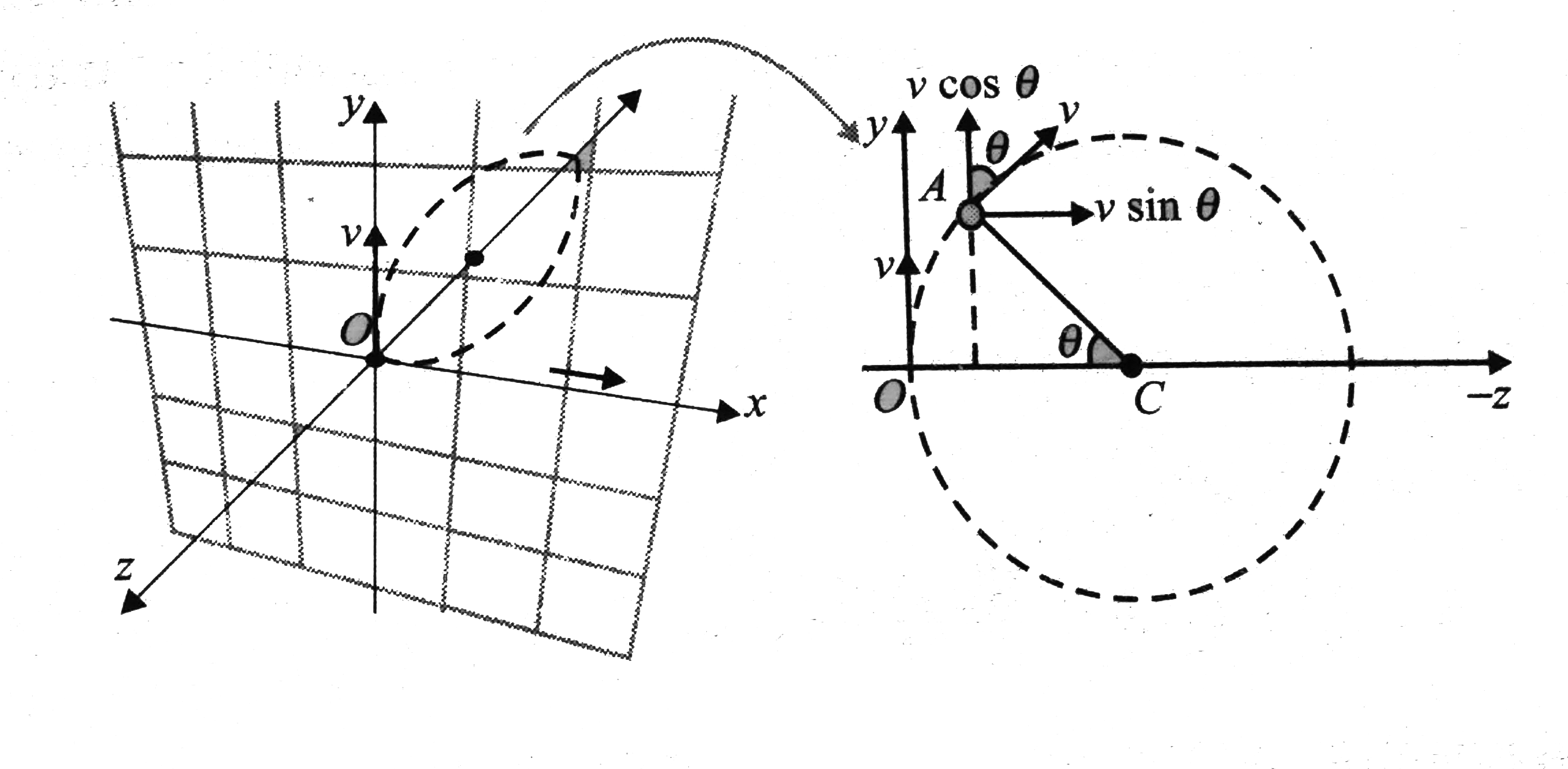
Writing velocity vector at time t.
→v=vcosθˆj−vsinθˆk
→v(t)=vcos(qBtm)ˆj−vsin(qBtm)ˆk
Now writing y and z coordinates of the particle.
y-coordinate of P=Rsinθ
z-coordinate of P=−(R−Rcosθ)
→r(t)=rsin.qBtmj−R(1−cos.qBtm)ˆk
[where R=mvqB].
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
In a right handed coordinate system XY plane is horizontal and Z-axis is vertically npward. A uniform magnetic field exist in space in vertically npward direction with magnetic induction B. A particle with mass m and charge q is projected from the origin of the coordinate system at t=0 with a velocity vector given as
→v=v1ˆi+v2ˆk
Find the velocity vector of the particle after time t.
View SolutionA particle of mass m and charge q is projected into a uniform magnetic field −−→B=−B0ˆK with velocity −−→V−V0ˆi from origin. The position vector of the particle at time t is −−→r. Find the impulse of magnetic force on the particle by the time −−→r.−−→V becomes zero for the first time.
View Solution
Knowledge Check
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2mThe velocity vector of the motion described by the position vector of a particle, r=2tˆi+t2ˆj is given by
Av=2ˆi+2tˆjBv=2tˆI+2tˆjCv=tˆi+t2ˆjDv=2ˆi+t2ˆjA particle of mass m and charge q travelling at a velocity v along x-axis at time t=0. It enters a region in which electric field, E is present along z-axis and magnetic field, B is present along y-axis. The distance covered upto time t=0.2×10−1sec, along x-axis is v/50 (in meters). find the value of v:
 A50EBBE50BCE20BDEB
A50EBBE50BCE20BDEB
A particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=πm2qB.
View SolutionIf in previous illustration, The charge particle is projected at angle α with x-axis with magnitude of velocity. Find
a. velocity vector in function of time →v(t).
b. position vector in function of time →r(t).

View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA particle of mass m is travelling with a constant velocity v=v0ˆi along the line y=b,z=0. Let dA be the area swept out by the position vector from origin to the particle in time dt and L the magnitude of angular momentum of particle about origin at any time t. Then
View SolutionThere exist uniform magnetic and electric fields of magnitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View Solution
