A particle of mass m and charge q is projected into a uniform magnetic field −−→B=−B0ˆK with velocity −−→V−V0ˆi from origin. The position vector of the particle at time t is −−→r. Find the impulse of magnetic force on the particle by the time −−→r.−−→V becomes zero for the first time.
The correct Answer is:2mv0ˆi
Step by step video, text & image solution for A particle of mass m and charge q is projected into a uniform magnetic field underset(B)to=-B_(0)hatK with velocity underset(V)to-V_(0)hati from origin. The position vector of the particle at time t is underset(r)to. Find the impulse of magnetic force on the particle by the time underset(r)to.underset(V)to becomes zero for the first time. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-2
13 Videos
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-3
4 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
- NUCLEAR PHYSICSBOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions
54 Videos
Similar Questions
A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
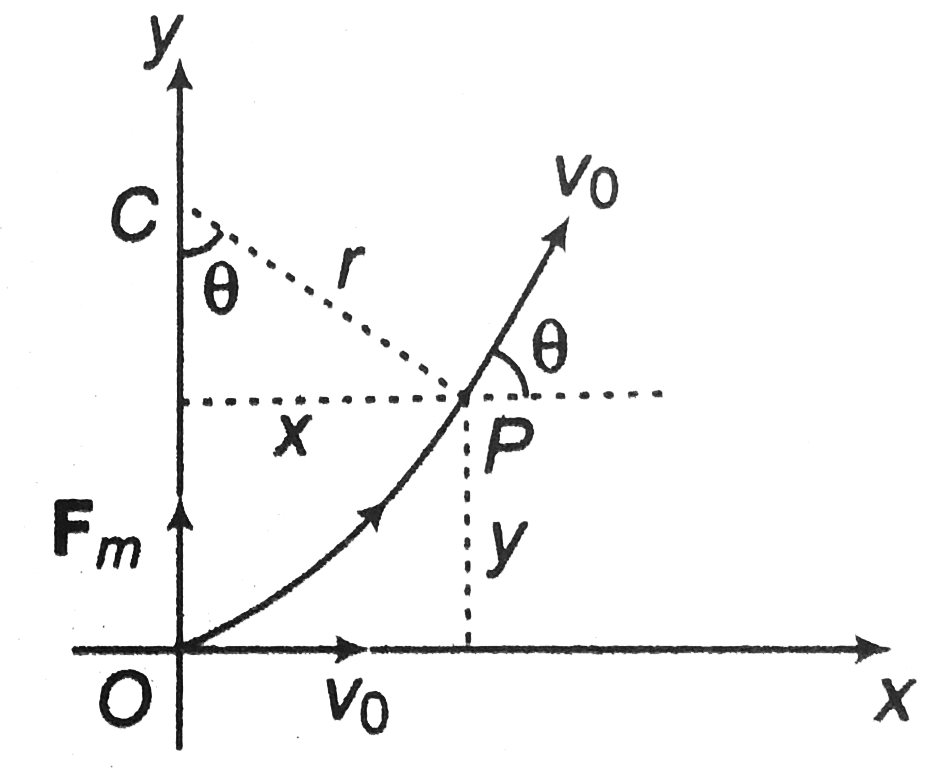
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View Solution
Knowledge Check
A particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
A−2mv0qB0Bmv0qBC−mv0qBD2mv0qB0A positive charge q is projected in magnetic field of width mv√2qB with velocity v as shown in figure. Then time taken by charged particle to emerge from the magnetic field is
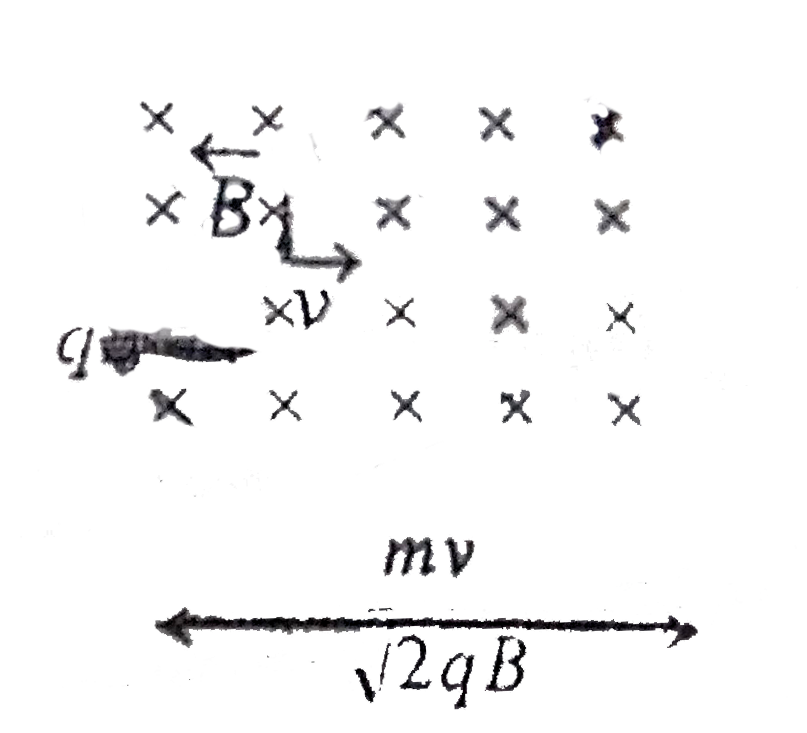 Am√2qBBπm4qBCπm2qBDπm√2qB
Am√2qBBπm4qBCπm2qBDπm√2qB
A particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA particle of charge q and mass m is prjected in a uniform and contant magnetic field of strength B.The initial velocity →v makes angle θ with the →B.Find the distance travelled by the particle in time t.
View SolutionA particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=πm2qB.
View SolutionA particle of mass m and charge + q is projected from origin with velocity →V=V0ˆi in a magnetic field →B=−(B0x)ˆk. Here V0 and B0 are positive constants of proper dimensions. Find the radius of curvature of the path of the particle when it reaches maximum positive x co-ordinate.
View SolutionA particle of mass m and charge q is moving in a region where uniform electric field −−→E and and uniform mag-netic field −−→Bare present. It is given that −−→E∣∣→E∣∣=−−→B∣∣→B∣∣. At time t = 0, velocity of the particle is −−→V0 and −−→V0.−−→E=0. Write the velocity of the particle at time t.
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.
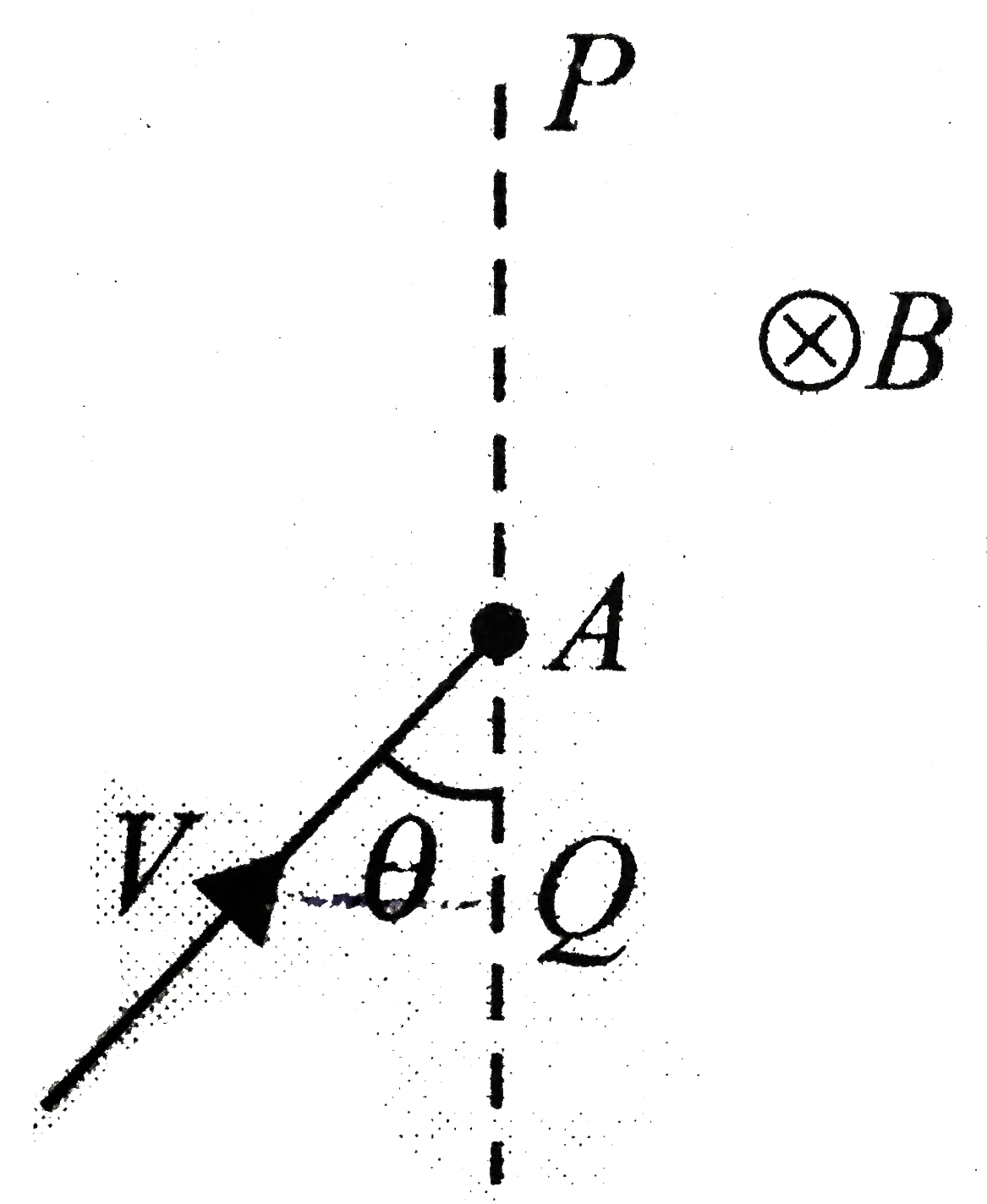
View Solution
