Consdier the equation
ddt[∫→F.d→s]=A[→F.→p] Then dimension of A will be (where →F= force, d→s= small displacement, t=time and →p= linear momentum).
M∘L∘T∘
M1L∘T∘
M−1L∘T∘
M∘L∘T−1
To find the dimension of A in the equation
ddt(→F⋅→s)=A(→F⋅→p)
where →F is force, →s is small displacement, t is time, and →p is linear momentum, we will proceed step by step.
Step 1: Determine the dimensions of →F⋅→s
The dot product →F⋅→s represents work done, which has the dimension of energy. The unit of force →F is Newton (N), and the unit of displacement →s is meter (m).
The dimension of force →F is given by:
(→F)=(M)(L)(T−2)
where M is mass, L is length, and T is time.
The dimension of displacement →s is:
(→s)=(L)
Thus, the dimension of →F⋅→s is:
(→F⋅→s)=(→F)(→s)=(M)(L)(T−2)(L)=(M)(L2)(T−2)
Step 2: Differentiate with respect to time
Now, we differentiate →F⋅→s with respect to time t:
ddt(→F⋅→s)
The dimension of this term is:
(ddt(→F⋅→s))=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
Step 3: Determine the dimensions of →F⋅→p
Next, we consider the right-hand side of the equation, A(→F⋅→p). The linear momentum →p is given by:
(→p)=(M)(L)(T−1)
Thus, the dimension of →F⋅→p is:
(→F⋅→p)=(→F)(→p)=(M)(L)(T−2)(M)(L)(T−1)=(M2)(L2)(T−3)
Step 4: Relate the dimensions in the equation
Now we can relate the dimensions in the equation:
(M)(L2)(T−3)=(A)(M2)(L2)(T−3)
Step 5: Solve for the dimension of A
To isolate A, we rearrange the equation:
(A)=(M)(L2)(T−3)(M2)(L2)(T−3)=(M−1)(L0)(T0)
Thus, the dimension of A is:
(A)=(M−1)(L0)(T0)
Final Answer
The dimension of A is:
Dimension of A=(M−1)
The dot product →F⋅→s represents work done, which has the dimension of energy. The unit of force →F is Newton (N), and the unit of displacement →s is meter (m).
(→F)=(M)(L)(T−2)
where M is mass, L is length, and T is time.
(→s)=(L)
(→F⋅→s)=(→F)(→s)=(M)(L)(T−2)(L)=(M)(L2)(T−2)
Now, we differentiate →F⋅→s with respect to time t:
ddt(→F⋅→s)
The dimension of this term is:
(ddt(→F⋅→s))=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
Next, we consider the right-hand side of the equation, A(→F⋅→p). The linear momentum →p is given by:
(→p)=(M)(L)(T−1)
Thus, the dimension of →F⋅→p is:
(→F⋅→p)=(→F)(→p)=(M)(L)(T−2)(M)(L)(T−1)=(M2)(L2)(T−3)
Now we can relate the dimensions in the equation:
(M)(L2)(T−3)=(A)(M2)(L2)(T−3)
To isolate A, we rearrange the equation:
(A)=(M)(L2)(T−3)(M2)(L2)(T−3)=(M−1)(L0)(T0)
(A)=(M−1)(L0)(T0)
The dimension of A is:
Dimension of A=(M−1)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The distance x of a particle moving in one dimensions, under the action of a constant force is related to time t by the equation, t=√x+3, where x is in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
View SolutionThe distance (x) particle moving in one dismension, under the action of a constant force is related to time (t) by equation t√x+3
where (x) is in vettres and (t) in seconds. Find the displacement of the particle when its velcity is zero.
View Solution
Knowledge Check
Consider the equation ddt(∫→F.d→S)=A(→F.→p) where →F≡ force, →s≡ displacement, t ≡ time and →p= momentum. The dimensional formila of A will be
AM0L0T0BML0T0CM−1L0T0DM0L0T−1Force on a particle in one-dimensional motion is given by F=Av+Bt+CxAt+D, where F= force, v= speed, t= time, x= position and A, B, C and D are constants. Dimension of C will be-
AM2L−2T0BML−1T0CM2L0T−2DNone of theseIn the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of 2×10−3kg/m that passes over a light pulley . The string is connected to a vibrator of frequency 700Hz and the length of the string between the vibrator and the pulley is 1m.

The string is set into vibrations and represented by the equation y=6sin(πx10)cmcos(14×103πt) where x ane y are in cm , and t in s, the maximum displacement at x=5m from the vibrator isA6cmB3cmC5cmD2cm
The displacement x of particle moving in one dimension, under the action of a constant force is related to the time t by the equation t=√x+3
where xis∈metersandt∈seconds . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first 6seconds.
View SolutionThe displacement x of a particle moving in one dimension under the action of a constant force is related to time t by the equation t=√x+3, where x is in meter and t is in second. Find the displacement of the particle when its velocity is zero.
View SolutionSeparation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a)n Show →p=→pi+mi→V where →pi is the momentum of the ith particle (of mass mi) and →pi=mi→vi, Not →vi is the velocity of the ith particle relative to the centre ofmass.
Also, prove using the definition of the centre of mass ∑→pi=0
(b) Show K=K'+1/2MV2 where K is the total kinetic energy of the system of particles, K is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system)
(c) Show →L=→L+→R×MV
where →L'=∑→ri×→pi is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember →ri=→ri−→R, reat of the notation is the standard notation used in the chapter. Note →L'andM→R×→V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show d→Ldt=∑→ri×d→p'dt Further show that d→L'dt=→τext' where Text is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton's Third Law. Assume the internal forces between any two particles aet along the line joining the particles.)
View SolutionSppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
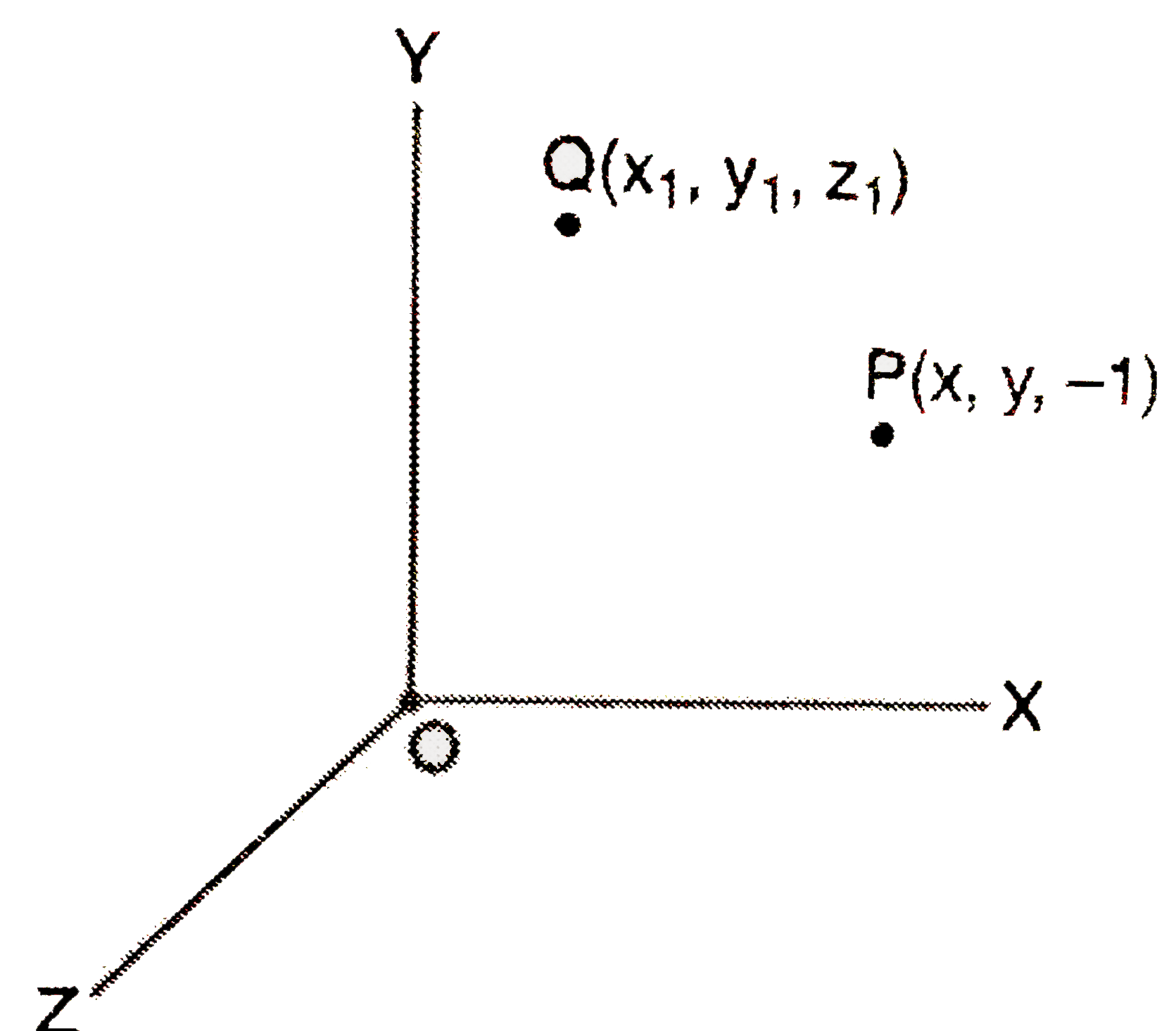
Answer the following questions.
Coordinates of P are :
View SolutionA particle moves in x-y plane under action of a path dependent force F=yˆi+xˆj. The work done by the force as it moves in x-y plane can be evaluated by solving the integral ∫→F.→dr,where →dr=dxˆi+dyˆj. The position coordinates x and y will vary according to some constraint determined by teh path followed by the particle. For example, if particle moves along a straight line from one position to other, then an possible rarticle. For example, if particle moves along a straight line from one position to other, then a possible relation is y=mx+c. NOw. try to solve the following questions.
1. The particel moves along a straight line from origin to (a ,a) . The work done by the force on the particle is
(1)a2 (2)2s (3)a22 (4)Zero
2. The particle moves from (0,0) to (a,0) and then from, (a,0) to (a,a), in straight line paths. The work done by the force on the particle is
(1)a2 (2)2a (3)a22 (4) Zero
3. The differential work by the given force over an elementary displacement is given as dW=→F.→dr=ydx+xdy
This can be expressed as dW=d(xy). From this, it can be inferred that the work done by the force
(1) Depends only on initial and final values of x and y
(2) Depends on initial and final values and on the path followed
(3) Is zero for any values of x and y
(4) Is zero when object returns to original position after following any path
View Solution