A particle of mass m begins to slide down on a fixed smooth sphere from the top, when it breaks off the sphere, the tangential accleration will be
2g/3
g
√53g
g2
mgcosθ=mv2R
mg(R−Rcosθ)
=12mv2
⇒cosθ=23
a1=gsinθ=g×√53
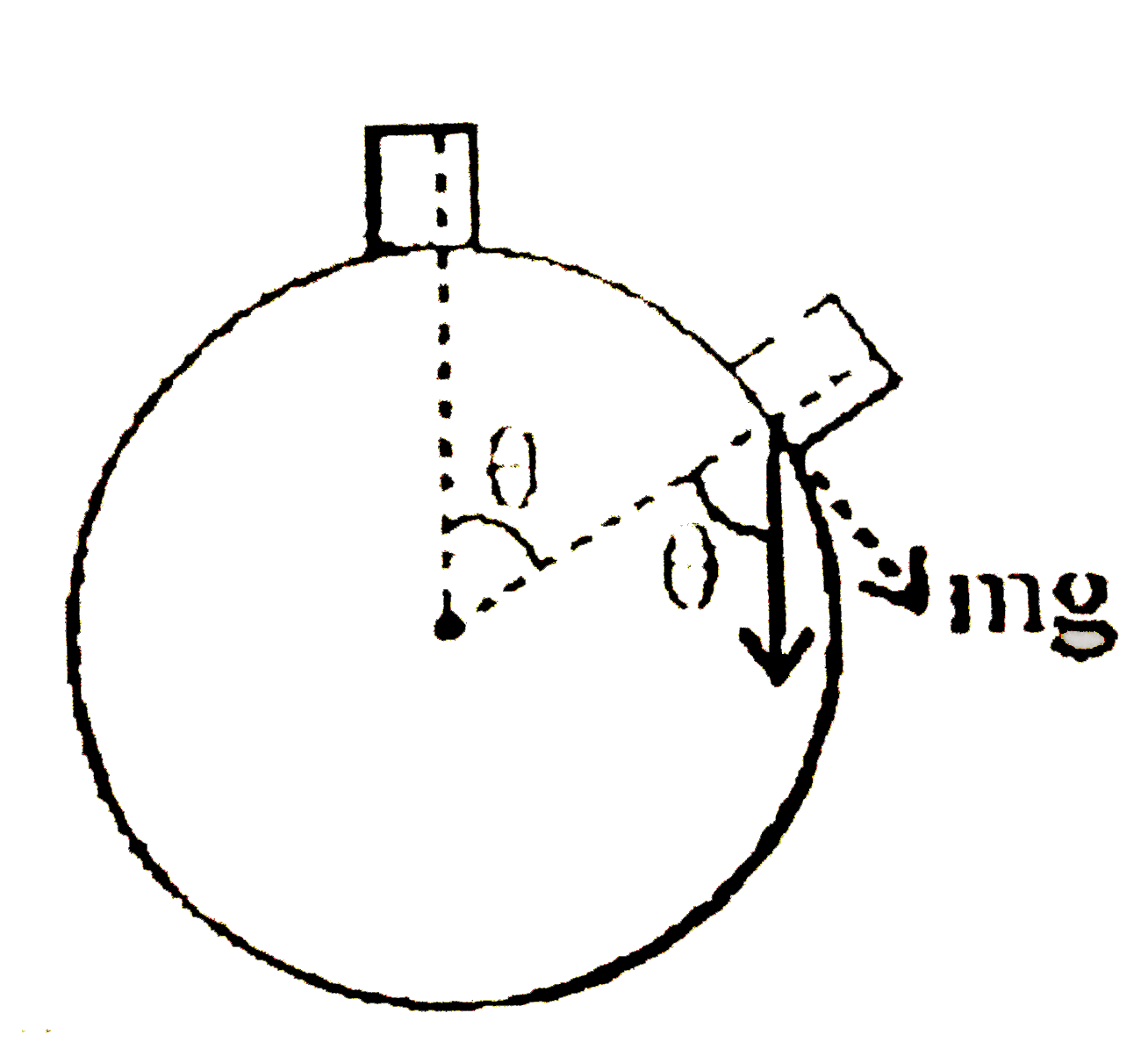
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle mass m begins to slide down a fixed smooth sphere from the top of its vertical diameter. Calculate its tangential acceleration, radial acceleration and total acceleration when it breaks off.
View SolutionA particle of mass m being to slide down a fixed smooth sphere from the top as shown. If its acceleration when it breaks off the sphere is 2a. The value of a is :
View Solution
Knowledge Check
A particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
A2g3B√5g3CgDg3A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gRA sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
Aconserved about every pointBconserved about the point of contact onlyCconserved about the centre of the sphere onlyDconserved about any point on a line parallel to the inclined plane and passing through the centre of the ball
A particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View Solution