A projectile is fired horizontally from an inclined plane (of inclination 45∘ with horizontal) with speed=50m/s. If g=10m/s2, the range measured along the incline is
500m
500√2m
200√2m
none of these
To solve the problem of finding the range of a projectile fired horizontally from an inclined plane at an angle of 45 degrees, we can follow these steps:
Step 1: Understand the problem
The projectile is fired horizontally with an initial speed u=50m/s from an inclined plane that makes an angle β=45∘ with the horizontal. The acceleration due to gravity is g=10m/s2.
Step 2: Identify the relevant formula
The range R of a projectile launched from an inclined plane can be calculated using the formula:
R=2u2sin(α+β)gcos2(β)
where α is the angle of projection (which is 0∘ since it is fired horizontally), and β is the angle of the incline.
Step 3: Substitute the values
In our case:
- u=50m/s
- α=0∘
- β=45∘
Substituting these values into the formula:
R=2×(50)2×sin(0+45∘)10cos2(45∘)
Step 4: Calculate the trigonometric values
We know:
- sin(45∘)=1√2
- cos(45∘)=1√2
Thus, cos2(45∘)=(1√2)2=12.
Step 5: Substitute the trigonometric values into the formula
Now substituting the trigonometric values into the equation:
R=2×(50)2×1√210×12
Step 6: Simplify the equation
Calculating the numerator:
2×(50)2=2×2500=5000
So,
R=5000×1√210×12=5000×1√25=1000√2
Step 7: Rationalize the denominator
To rationalize the denominator:
R=1000×√22=500√2
Final Answer
Thus, the range measured along the incline is:
R=500√2meters
The projectile is fired horizontally with an initial speed u=50m/s from an inclined plane that makes an angle β=45∘ with the horizontal. The acceleration due to gravity is g=10m/s2.
The range R of a projectile launched from an inclined plane can be calculated using the formula:
R=2u2sin(α+β)gcos2(β)
where α is the angle of projection (which is 0∘ since it is fired horizontally), and β is the angle of the incline.
In our case:
- u=50m/s
- α=0∘
- β=45∘
R=2×(50)2×sin(0+45∘)10cos2(45∘)
We know:
- sin(45∘)=1√2
- cos(45∘)=1√2
Now substituting the trigonometric values into the equation:
R=2×(50)2×1√210×12
Calculating the numerator:
2×(50)2=2×2500=5000
So,
R=5000×1√210×12=5000×1√25=1000√2
To rationalize the denominator:
R=1000×√22=500√2
Thus, the range measured along the incline is:
R=500√2meters
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View Solution
Knowledge Check
A particle is fired horizontally form an inclined plane of inclination 30∘ with horizontal with speed 50ms−1. If g=10ms−2 , the range measured along the incline is
A500mB10003mC200(√2) mD100(√3) mA body of mass 5kg is moved up over 10m along the line of greatest slope of a smooth inclined plane of inclination 30∘ with the horizontal. If g=10m/s2, the work done will be
A500 JB2500 JC250 JD25 JA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
A415B45(1√3−13)C45(1√3−13)D4√3(1√3−13)
A block of mass 10 kg rests on a rough inclined plane of inclination 45∘ with the horizontal. What minimum force is required to just move the block up the inclined plane. Given μs=0.5andg=10ms−2.
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is thrown horizontally with velocity 10 m/s from an incline of inclination 30∘ , it hits on the incline agin then displacement (in m) of the particle is:
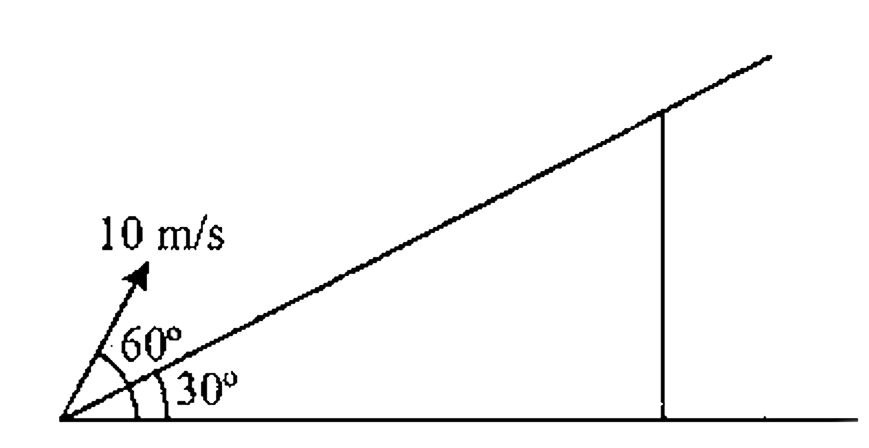
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
View SolutionA wooden box of mass 8kg slides down an inclined plane of inclination 30∘ to the horizontal with a constant acceleration of 0.4ms−2 What is the force of friction between the box and inclined plane ? (g=10m/s2) .
View Solution
