Two blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:

the heavier mass reaches the bottom in a shorter time
both the masses have the same kinetic energy on arriving at B
the heavier mass has twice the momentum than that of the other when reaching B
the lighter mass reaches the bottom in a shorter time
a=gsinθ−μgcosθ is same for (1) and (2) both will read bottom with same speed
u2=0+2as
K1=12(2m)v2t
K2=12(m)v22
k_(1)cancel=k_(2)
p1=2mv1,p2=mv2
p1=2p2
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionConsider a block of mass m that slides down the different inclined planes having same base legth L and same coefficient of friction.
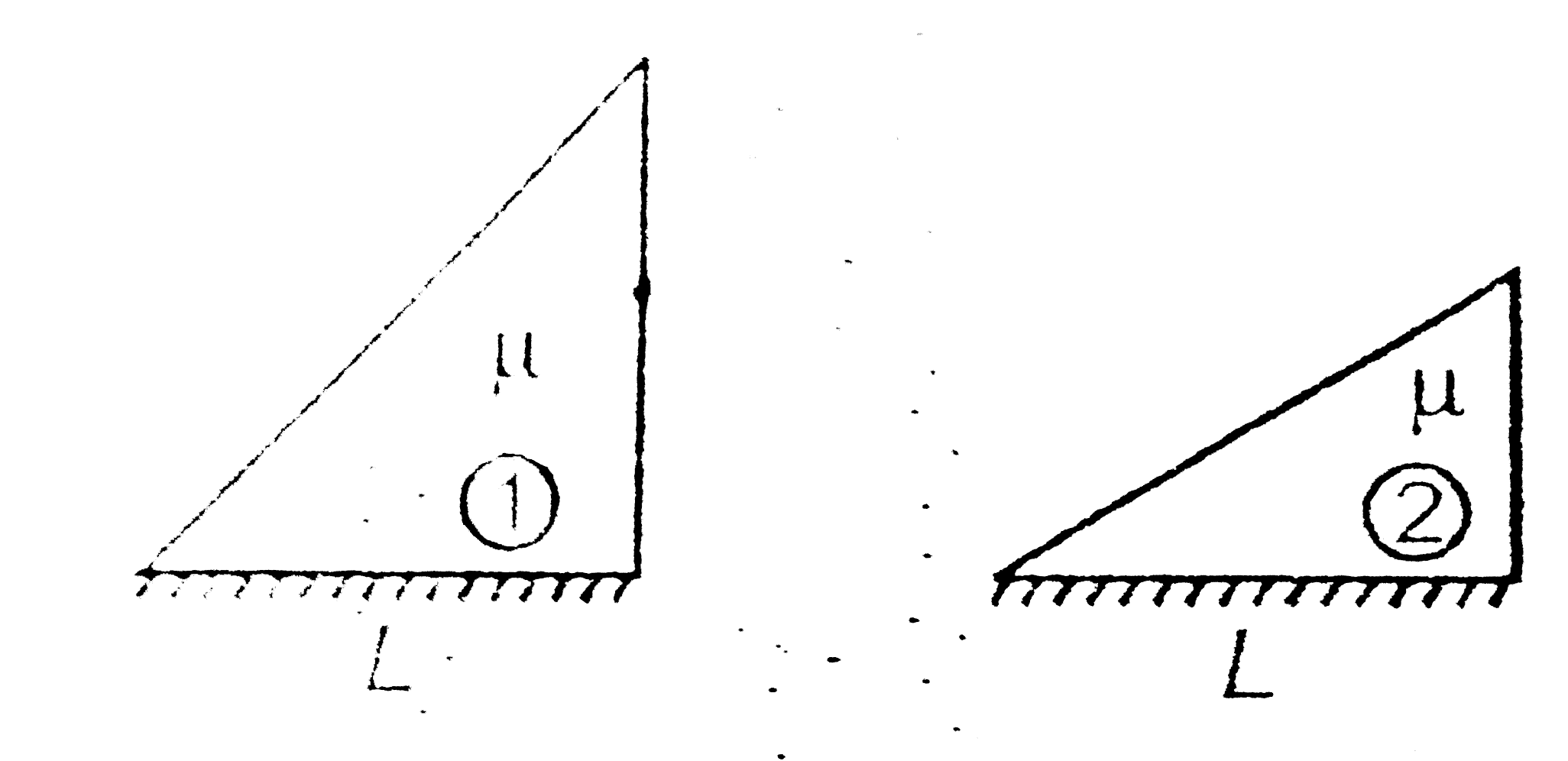
STATEMENT-1 Work done by force of friction will be same for the motion of the two inclined planes.
STATEMENT-2 Frictional force is a conservation force.
View Solution
Knowledge Check
Two blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)gA block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
AmgBmgcosθCmgsinθDmgtanθA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Ag(sinθ+√2μkcosθ)Bg(sinθ+μkcosθ)Cg(sinθ−√2μkcosθ)Dg(sinθ−μkcosθ)
Two blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
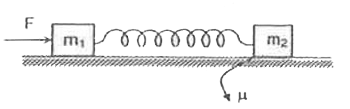
View SolutionA block of mass m slides down with uniform speed on an inclined plane having inclination θ If the coefcient of friction between the inclined plane and the block is then the contact force between them is
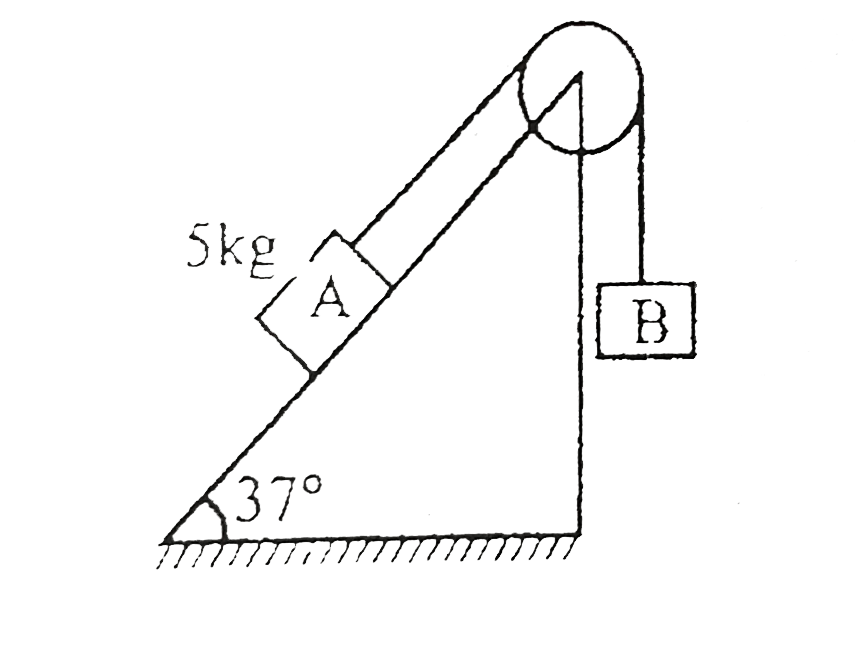
View SolutionTwo blocks A and B are connected by as string as shown in figure. Friction coefficient of the incline plane and block is 0.5. The mass of the block A is 5kg. If minimum & maximum values of masses of the block B for which the block remains in equilibrium are m1 & m2 then find value of (m2−m1).
View Solution