A projectile si thrown with velocity of $50 m / s$ towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is $53^{\circ}$ with the horizontal and the inclined plane is inclined at an angle of $45^{\circ}$ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $t = 7 sec$ , (b) $175 m$

$v_{x} = u_{x} = 50 {cos 53}^{\circ} = 30 m / s$
at striking point $v_{y} = - u_{x} = - 30 m / s$
(a) form time of flight
$v_{y} = u_{y} + a_{y} t \Rightarrow - 30 = 40 + (- 10) t \Rightarrow t = 7 sec$ ltbrltgt (b) for distance
distance $= O Q - M Q = u_{x} t - (u_{y} t + \frac{1}{2} a_{y} t^{2})$
distance $= 30 \times 7 - [40 \times 7 + \frac{1}{2} \times (- 10) \times 7^{2}]$
distance $= 210 - (280 - 245) \Rightarrow d i s tan c e$ = 175 m

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of $60^{\circ}$ with the horizontal its range on the inclined plane inclined at an angle of $30^{\circ}$ with the horizontal is
A21dm
B2.1dm
C30dm
D6dm
Question 2 - Select One
a particle is projected down on inclined plane with a velocity of 21m/s at an angle of $60^{\circ}$ with the horizontal its range on the inclined plane inclined at an angle of $30^{\circ}$ with the horizontal is
A21dm
B2.1dm
C30dm
D6dm
Question 3 - Select One
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

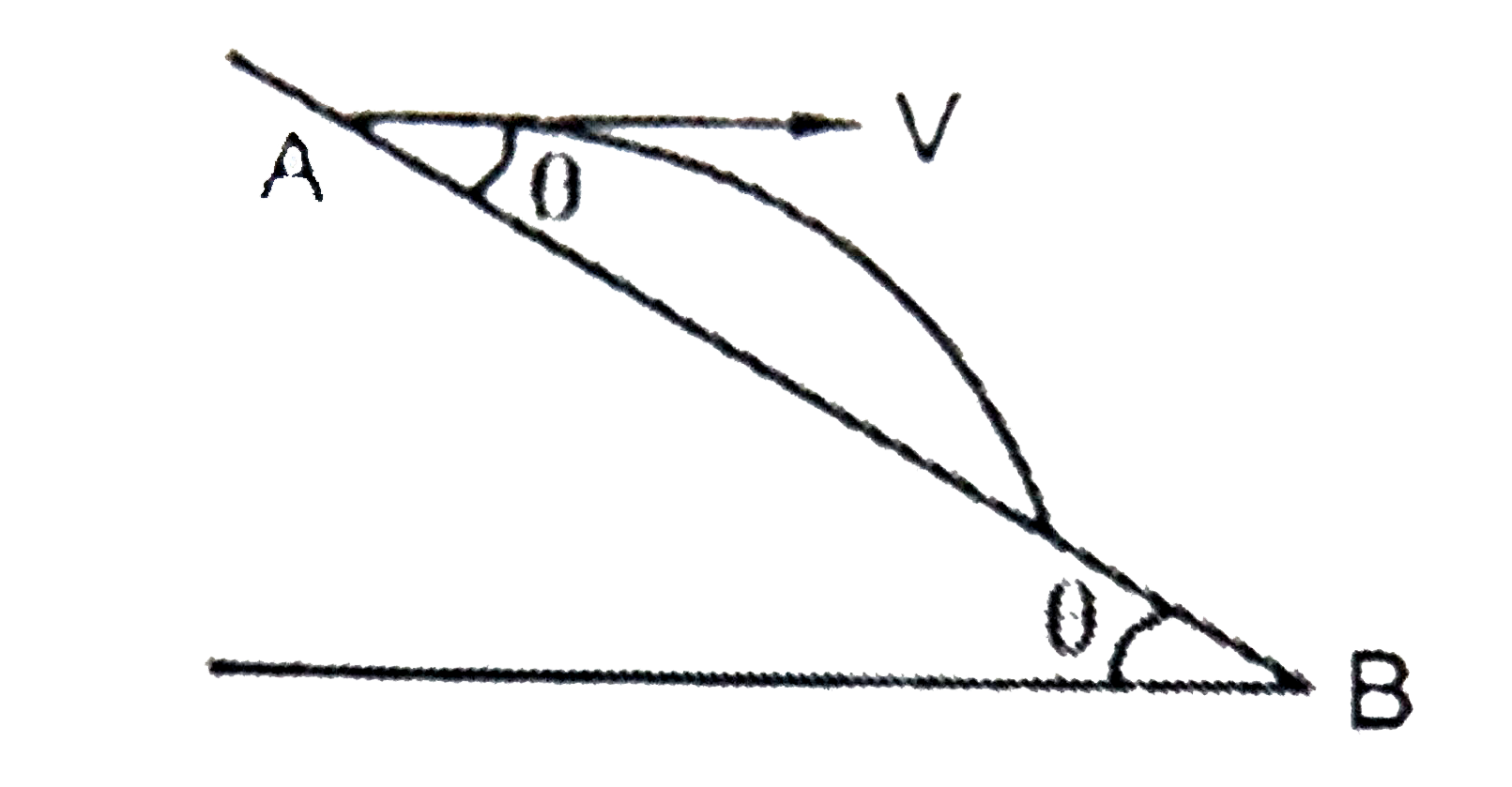
Find the time taken by the particle to hit the plane.
A $\frac{3}{4} s$
B $3 s$
C $4 s$
D $\frac{4}{3} s$

Recommended Questions

Home
Ask Doubt
Profile