A particle is projected with a velocity '9m/sec' at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the position 'x=R/3' (R-Range of the projectile).
3√20m
3√10
3√102m
34√10m
The correct Answer is:A, B, C
The equation of the trajectory of the projectile is,
y=xtanθ(1−xR). Here θ=45∘
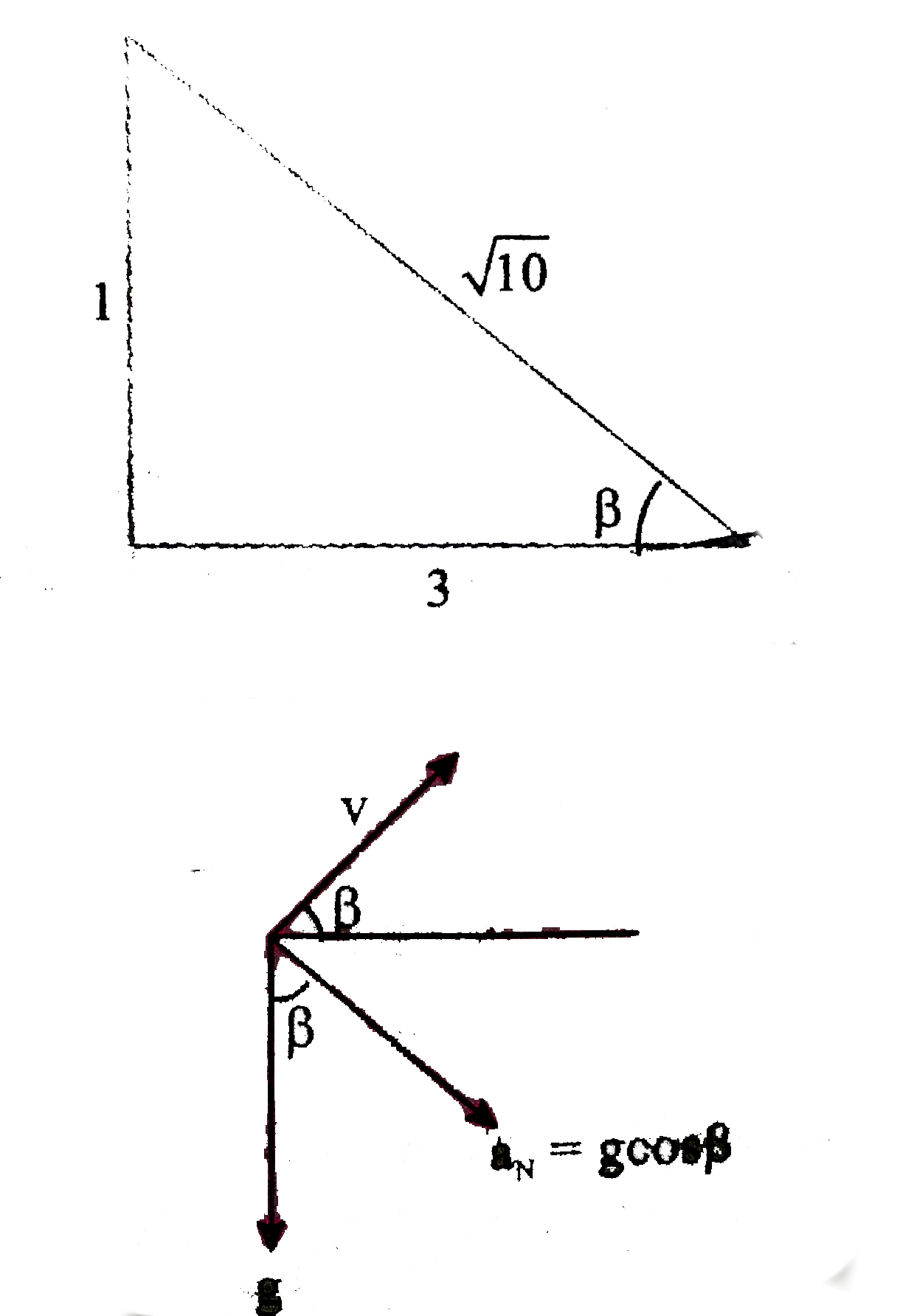
Let 'β' be the angle made by the instantaneous velocity vector with the horizontal at position x=R/3
m=tanβ=dydx=1−2xR=1/3
Let v be the velocity of the projectile at that instant
vcosβ=ucos45⇒v×3√10=u×1√2
⇒u=√10×u3√2
aN=gcosβ=v2R
∴R=v2gcosβ=10×u29×2×10×3√10
=9×99×2×3×√10=3√102
Topper's Solved these Questions
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL-VI
Explore 14 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL-VI PASSAGE
Explore 3 Videos
- CALORIMETRYBook:NARAYNAChapter:CALORIMETRYExercise:Level- II (H.W)
Explore 11 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
Similar Questions
If a particle is projected with a velocity 49m/sec. making an angle 60∘ with the horizontal, its time of flight is given by
View SolutionA particle is projected with a velocity →v=aˆi+bˆj. Find the radius of curvature of the trajectory of the particle at the (f) point of projection (ii) highest point.
View Solution
Knowledge Check
A particle is projected with a velocity 8m/sec at an angle 450, with the horizontal.What is the radius of curvature of the trajectory of the particle at the instant of '14th' of the time of ascent.
A6.25mB12.5mC8mD10mA heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A B
B C
C D
D
A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as
A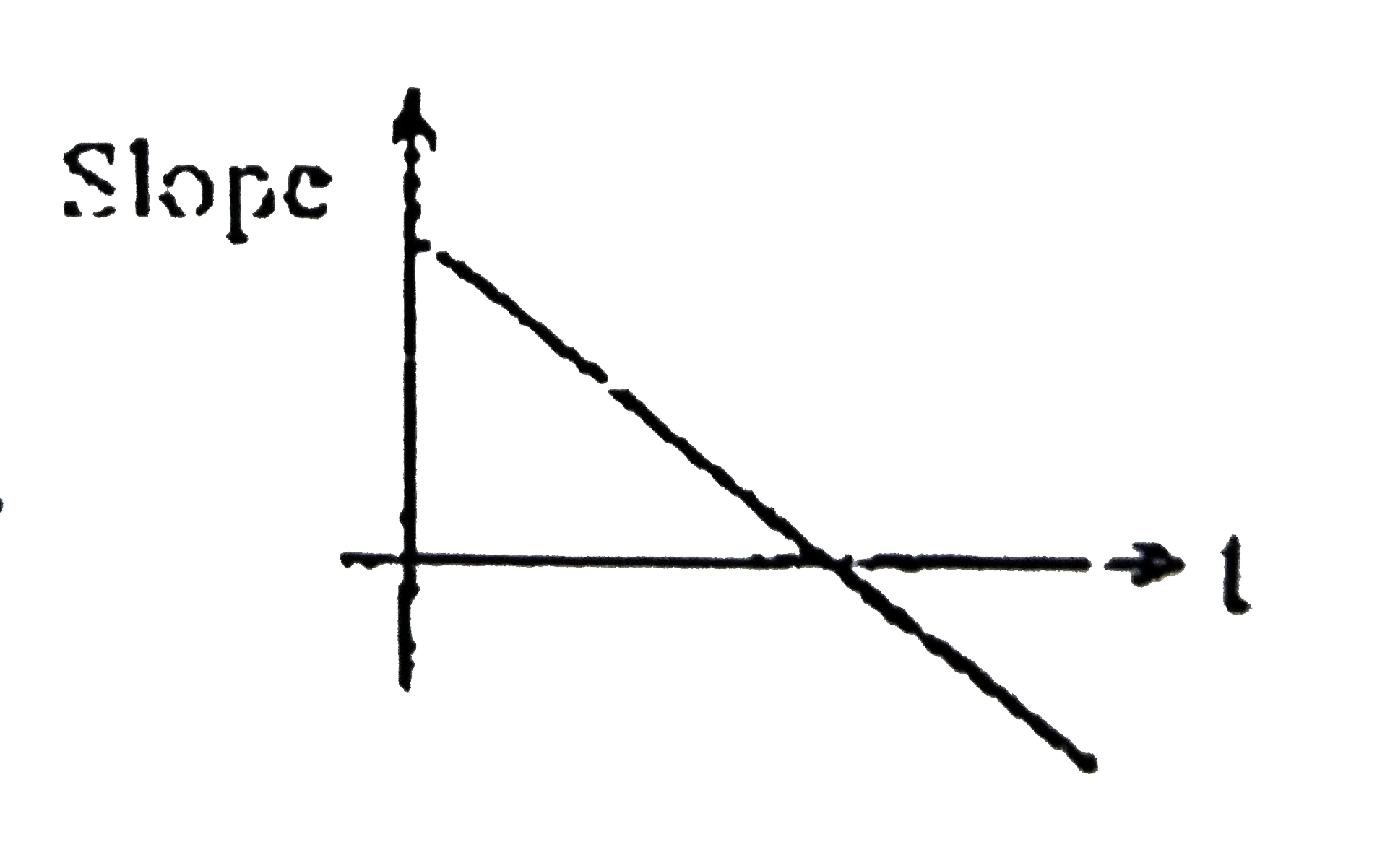 B
B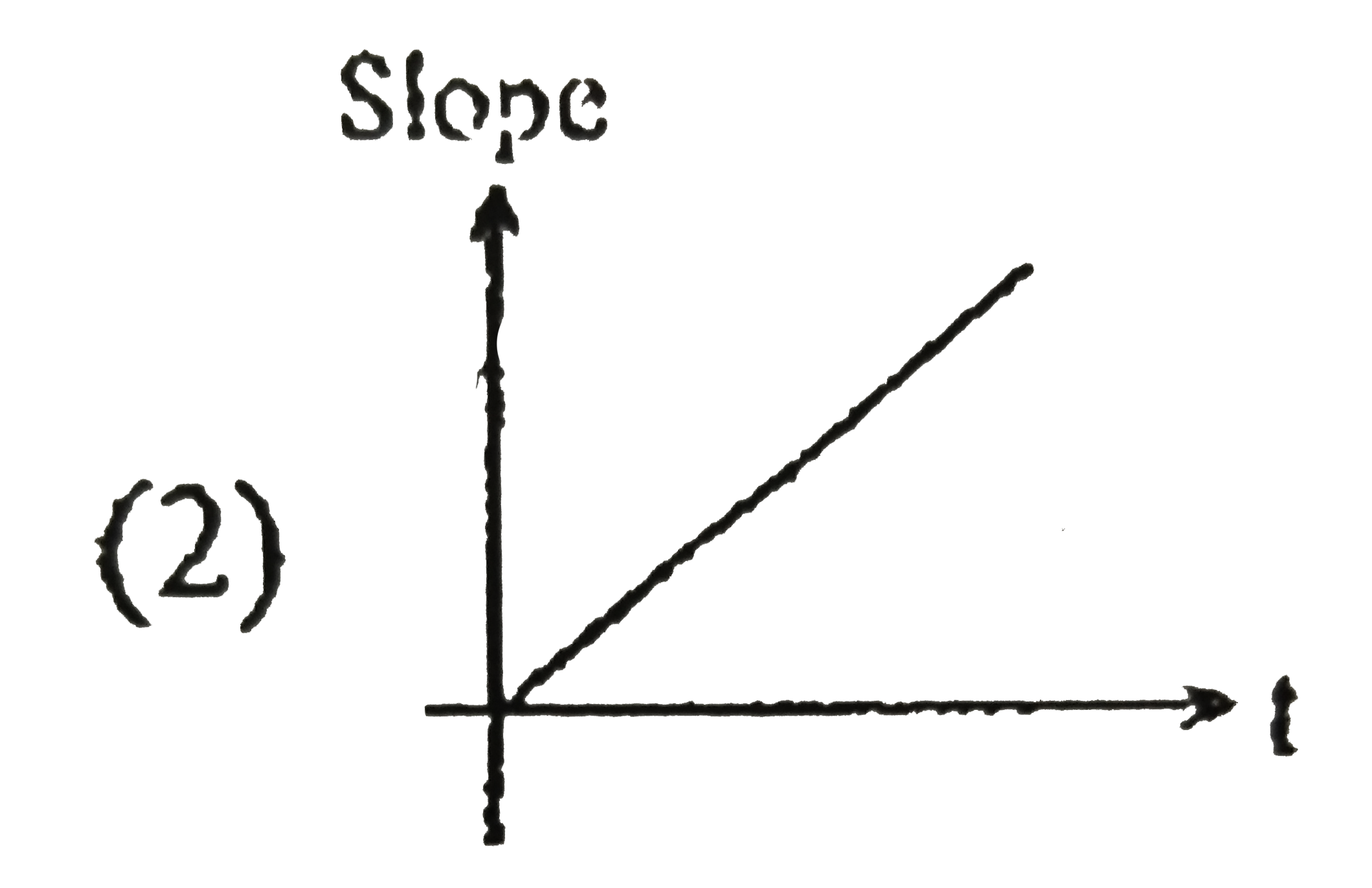 C
C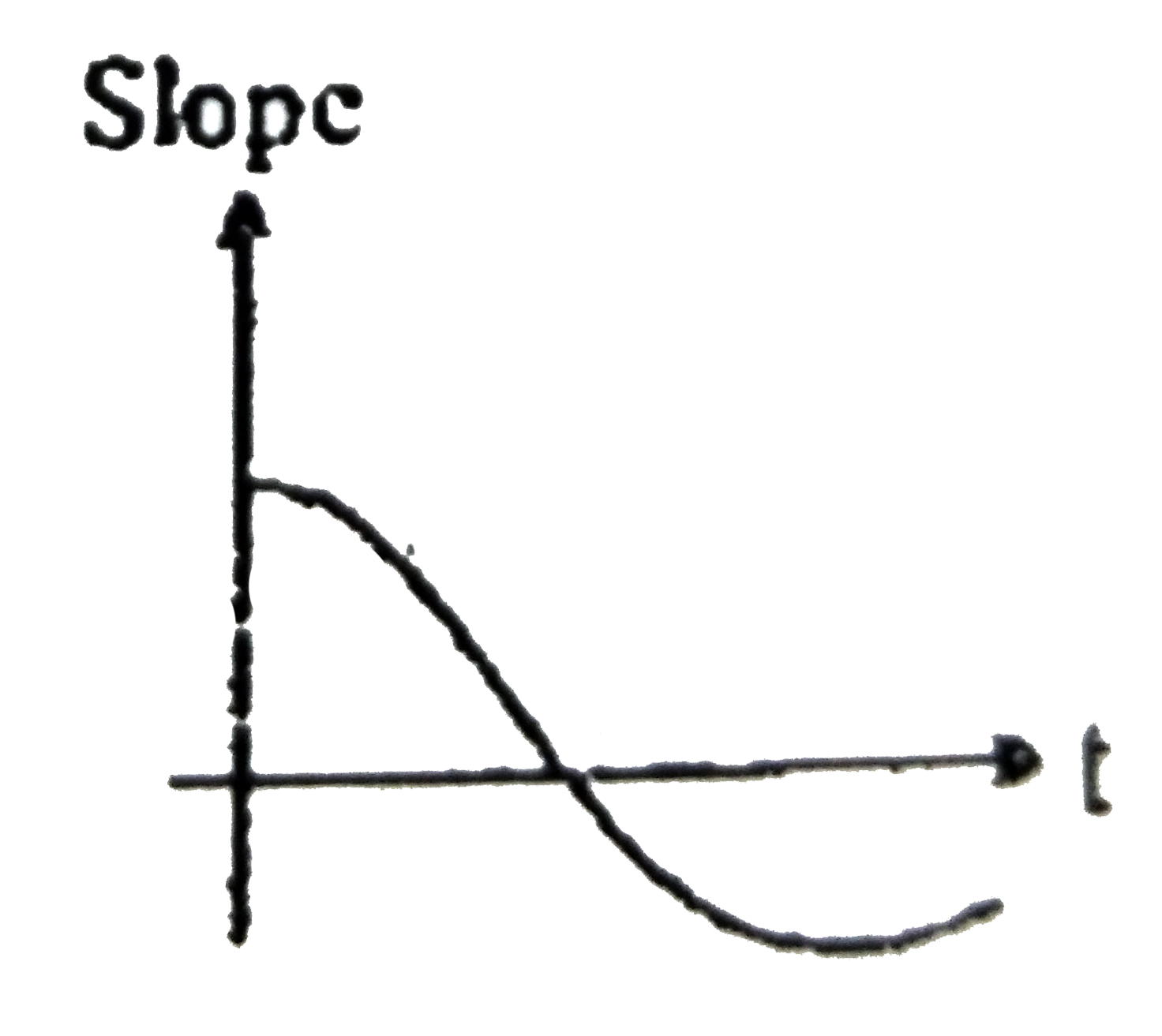 D
D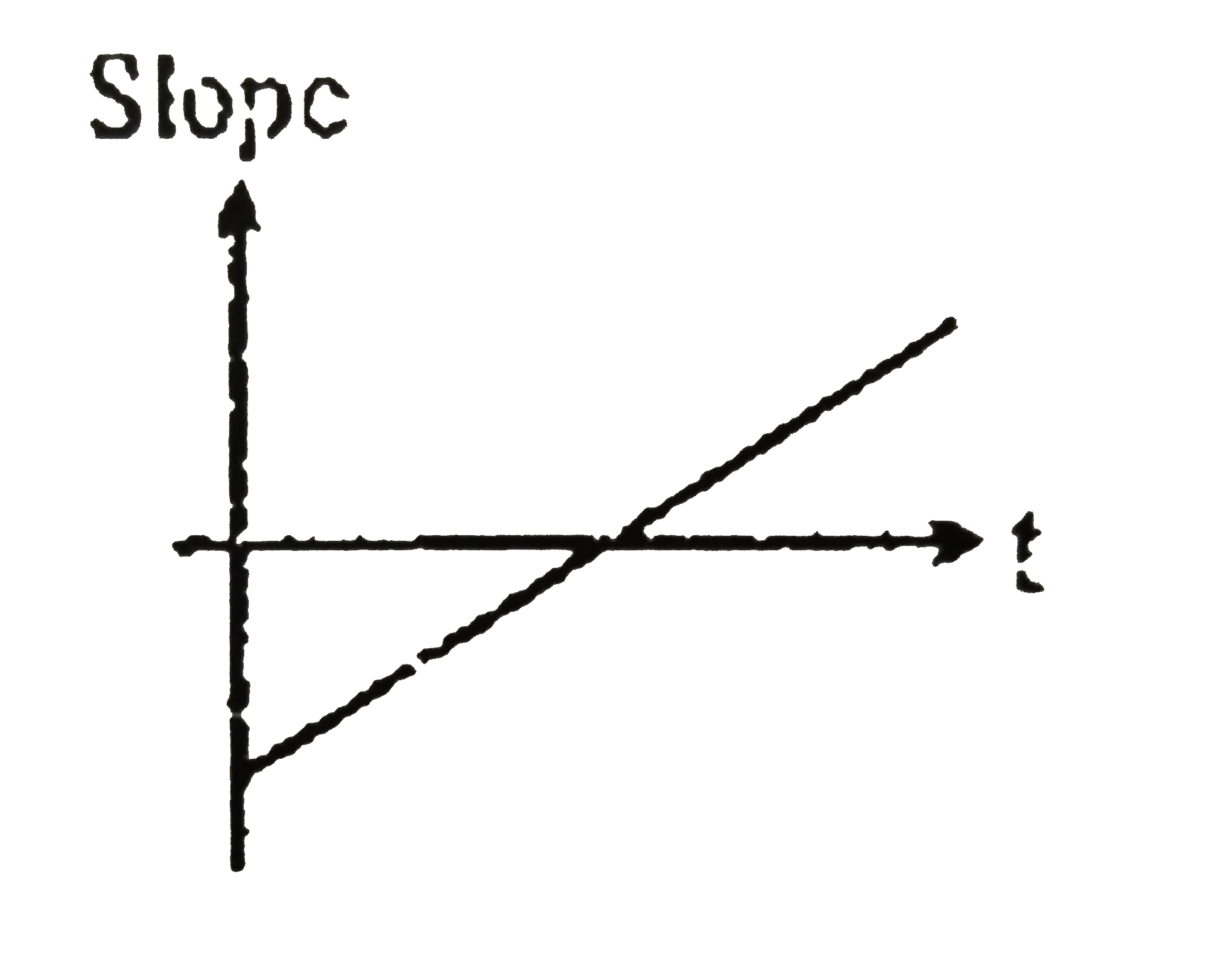
A particle is projected with a speed u at an angle 60∘ with the horizontal.What is the radius of curvature of the parabola traced out by the projectile at a point where the particle velocity makes an angle 30∘ with the horizontal?
View SolutionA particle is projected with a velocity of 39.2m/sec at an angle of 30∘ to the horizontal. It will move at right angles to the direction of projection after the time
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA projectile is projected at a angle 60∘ with horozontal with speed 10 m/s. The minimum radius of curvature of the trajectory described by the projectile is
View Solution
