A wooden stick of length L, radius R and density ρ has a small metal piece of mass m ( of negligible volume) attached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density σ(>ρ).
The correct Answer is:mmin=πr2l (√pσ−p);if tilted then it's axis should become verticl. C.M. should be lower than centre of bouyancy.
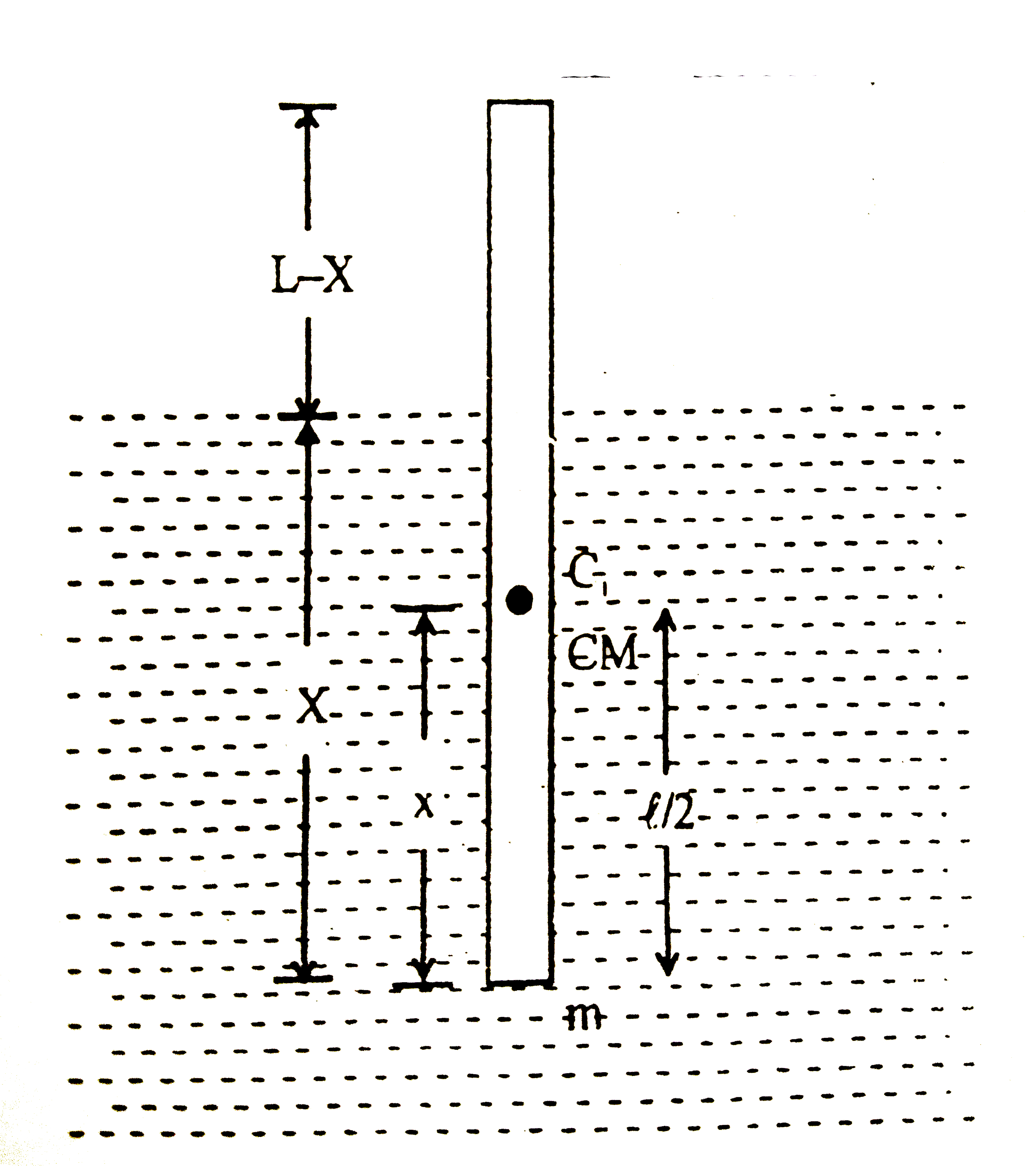To float wooden stick in vertical equalibrium it centre of Bnoynacy must be above centre of mass.
C1 is the centreof mass of wooden and CM is centre of mass of m and wooden stick.
x=m1x1+m2x2m1+m2⇒x=πR2Lρ×L2(πR2Lρ+m)
x=πR2L2ρ2(πR2Lρ+m) ....(1)
For suberged length X is liquid W=B
(m+πR2Lρ)g=πR2Xσg
X=m+πR2LρπR2σ ....(2)
Centre of Buoyancy will be at X2 .....(3)
For Equilibrium ,X2≥x
12(m+πR2LρπR2σ)≥πR2L2ρ2(m+πR2Lρ)
m+πR2Lρ≥πR2L2√ρσ ⇒m≥πR2Lρ(√ρσ−ρ)
mmin=πR2L(√ρσ−ρ)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - EXERCISE # III
18 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - MCQ & Solution
86 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - EXERCISE # I
21 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
Similar Questions
Two non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.
(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View SolutionA mass m is taken to a height R from the surface of the earth and then is given a vertical velocity υ. Find the minimum value of υ, so that mass never returns to the surface of the earth. (Radius of earth is R and mass of the earth m).
View Solution
Knowledge Check
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
A(a) The net elongation of the spring is 4πR3ρg3kB(b) The net elongation of the spring is 8πRρg3kC(c) The light sphere is partially submergedD(d) The light sphere is completely submergedA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
A√2σπρlgB√2σlπρgC√σπρgD√2σπρgA wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
A(σ−ρσ)mgB(σ−ρρ)mgCρmgσDσmgρ
A rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
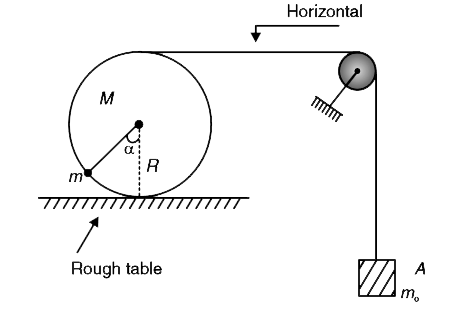
View SolutionA hollow cylindrical pipe of mass M and radius R has a thin rod of mass m welded inside it, along its length. A light thread is tightly wound on the surface of the pipe. A mass m0 is attached to the end of the thread as shown in figure. The system stays in equilibrium when the cylinder is placed such that α=30∘ The pulley shown in figure is a disc of mass M2
(a) Find the direction and magnitude of friction force acting on the cylinder.
(b) Express mass of the rod ‘m’ in terms of m0
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.
3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
What is the time period of the SHM as mentioned in previous question?
View SolutionA mass m is attached to the end of a rod of length l. The mass goes along a vertical circular path with the other end, hinged at its centre . What should be the minimum speed of mass at the bottom of this circular path
View Solution