A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
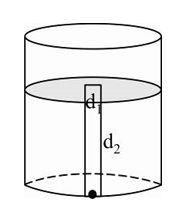
The correct Answer is:w=√3g2L(d2−d1d1)
τ=−(B−W)L2sinθ⇒τ=−(ALd2g−ALd1g)L2sinθ
For small θ
τ=−AL2g2(d2−d1)θ⇒Iα=−AL2g(d2−d1)2θ
α=−AL2g(d2−d1)2Iθ⇒α=−AL2g(d2−d1)2×ML23θ
α=−3AL2g(d2−d1)θ2ALd1L2=α=−(3g)(d2−d1)2Ld1θ
ω=√3g(d2−d1)2Ld1

Topper's Solved these Questions
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # III
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:MCQ & Solution
Explore 86 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # I
Explore 21 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
Similar Questions
A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .

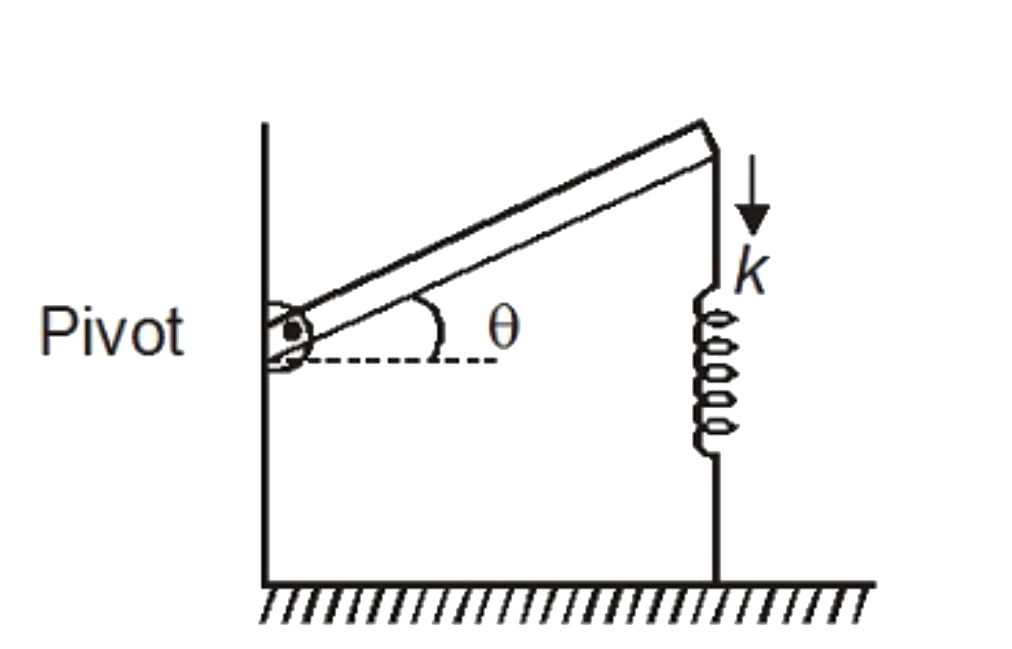
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion isA√3kmB√k3mC√3km+3g2LD√km
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθ
A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View Solutionif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solution

