A rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
2π√m+Lρ.Ak+Aρg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-I)
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-I) (Assertion Reasoning type)
Explore 3 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Subjective) (Level)
Explore 20 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
View SolutionA uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3g
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
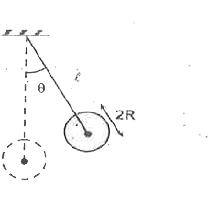
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionTwo rods AB and BC of equal cross-sectional area A and Young's constant Y1 and Y2 are joined and suspended from a fixed support A. A block of mass M is attached to the lowest point C. The density of the rods is negligibly small. Find displacement of the point C.

View Solution

