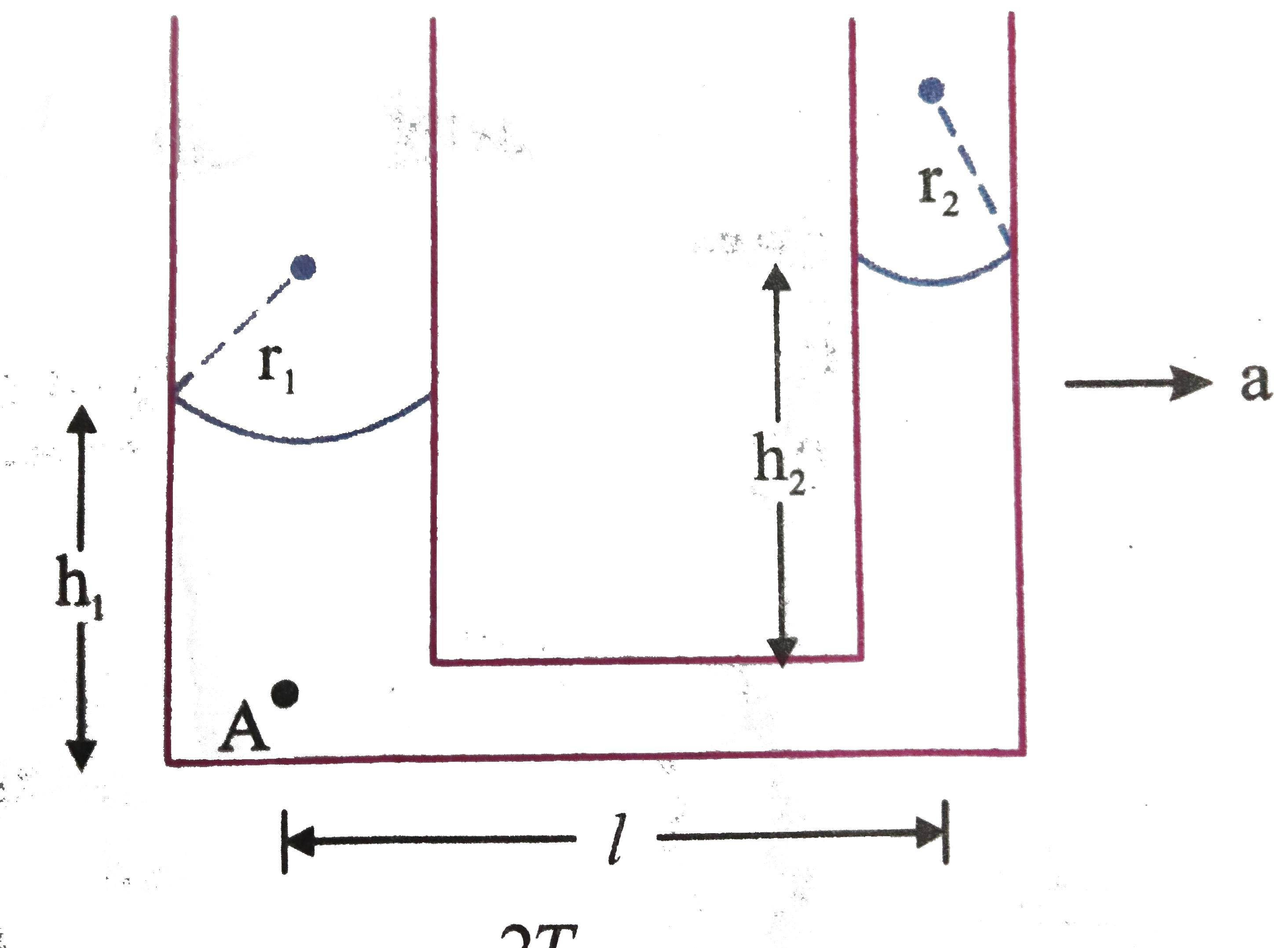
A vertical communicating tube contains a liquid of density $ρ$ . If it moves with a horizontal acceleration $a$ , pressure at $A$ is equal to :

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{8 h}{7}$

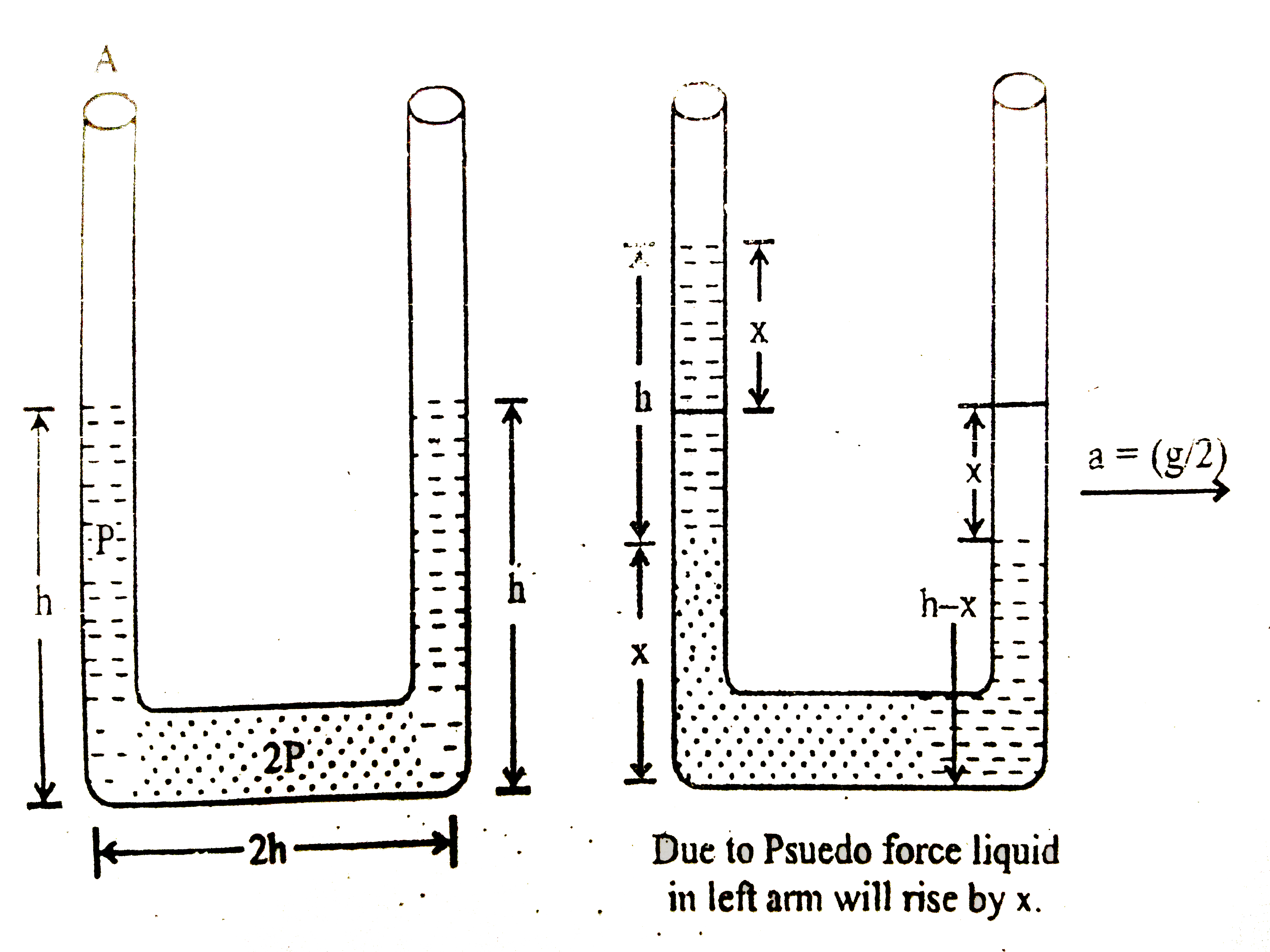
For equalibrium
$[h ρ g + x (2 ρ) g] = P_{p s u e d o} + (h - x) ρ g$
$h ρ g + 2 x ρ g = [(2 h - x) 2 ρ (g / 2) + x ρ (g / 2)] + (h - x) ρ g$
$h ρ g + 2 x ρ g = 2 h ρ g - \frac{x ρ g}{2} + x ρ g + h ρ g - x ρ g$
$\frac{7}{2} x ρ g = 2 h ρ g$
$x = \frac{4 h}{7}$
Difference in height $= 2 x = \frac{8 h}{7}$

|

Updated on:21/07/2023

Class 12 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

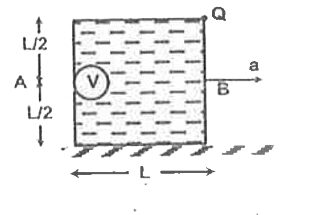
A sealed tank containing a liquid of density $ρ$ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
A $h ρ g$
B $l ρ a$
C $h ρ g - l ρ a$
D $h ρ g + l ρ a$
Question 2 - Select One
A sealed tank containing a liquid of density $ρ$ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points $A$ and $B$ will be

A $h ρ g$
B $l ρ g$
C $h ρ g - l ρ a$
D $h ρ g - l ρ a$
Question 3 - Select One
A beaker containing a liquid of density $ρ$ moves up with an acceleration $a$ . The pressure due to the liquid at a depth h below the free surface of the liquid is.
A $h ρ g$
B $h ρ (g + a)$
C $h ρ (g - a)$
D $2 h ρ g (\frac{g - a}{g + a})$

BANSAL-FLUID MECHANICS-EXERCISE # II

Home
Ask Doubt
Profile