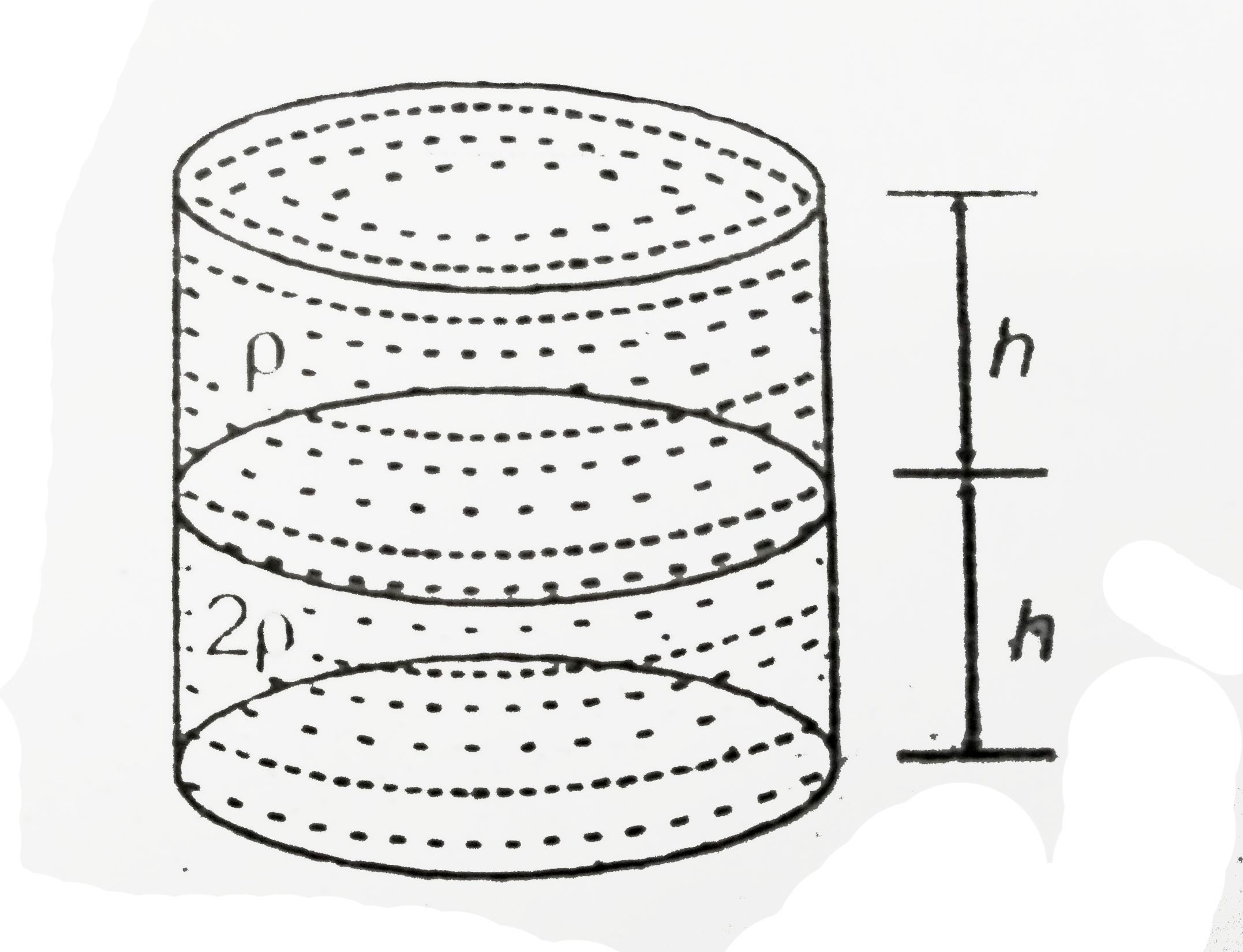
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
The correct Answer is:(a)(i)D=54d,(ii)p=P0+14(6H+L)dg;(b)(ii)x=√h(3H−4h)(iii)xmax=34H

W=B
A5LDg=[L4×A5×2d×g+3L4×A5×d×g]
D5=[d10+3d20]⇒D=54d
(b) P=(Pressure due to weight of liquid and cylinder on base + atmospheric pressure)
=[H2×A×d+H2×A×2d+L×A5×5d4]×gA+P0
=[3Hd2+Ld4]g+P0=(6H+L)4dg+P0
(b) (i) Applying Burnouli's theorem at interface of liquid and at tiny hol at bottom
[P0+(H2dg)+(H2−h)2dg]+0=P0+12(2d)v2+0
P0+H2dg+Hdg−2hdg=P0+dv2
(3H−4h)2dg=dv2
v=√(3H−4h)g2
(ii) x=vt⇒x=√(3H−4h)g2×√2hg⇒x=√h(3H−4h)
(iii) For x to be maximum
dxdh=0ordh(3H−4h)dh=0⇒h=3H8
Xmax=√3H8(3H−4×3H8)
Xmax=3H4
Topper's Solved these Questions
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # III
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:MCQ & Solution
Explore 86 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # I
Explore 21 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
View Solution_E01_201_Q01.png)
A piston of mass M=3kg and radius R=4cm has a hole into which a thin pipe of radius r=1 cm is inserted the piston can enter a cylinder tightly and without friction an initially it is at the bottom of the cylinder 750 gm of water is now poured into the pipe so that the piston&pipe and lifted up as shown find the height H of water in the cylinder and height h of water in the pipe.
View SolutionThe manifestation of band structure in solids is due to
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P_0 . Then density D of solid is given by
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View Solution