In the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
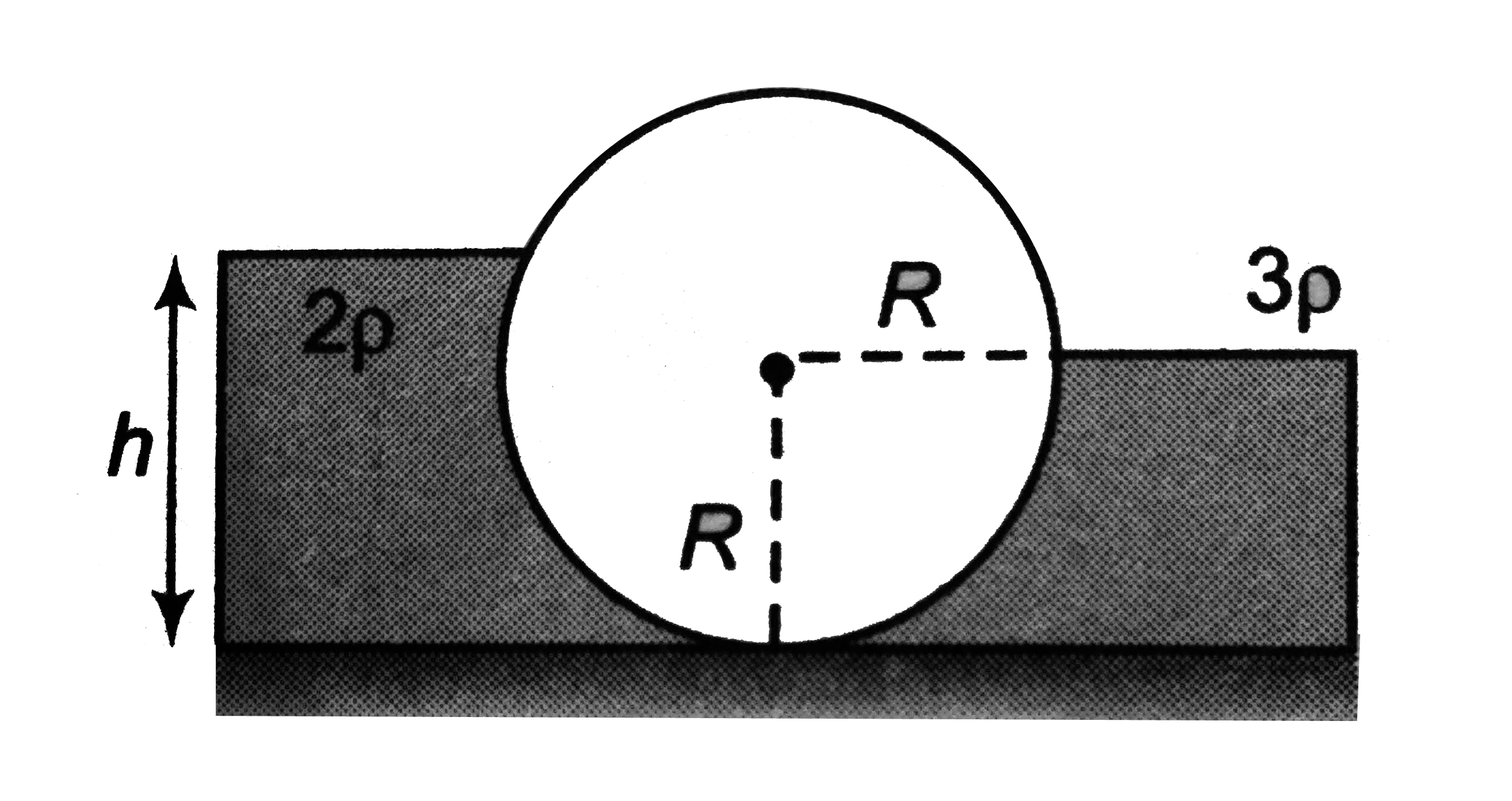
The correct Answer is:R√32
For equilibrium of cylinder Fx should be balanced
P3ρ×RL=P2ρ×hL
R(3ρ)g2×RL=h(2ρ)g2×hL
3R2=2h2
h=√32R
Topper's Solved these Questions
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # III
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:MCQ & Solution
Explore 86 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # I
Explore 21 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
Similar Questions
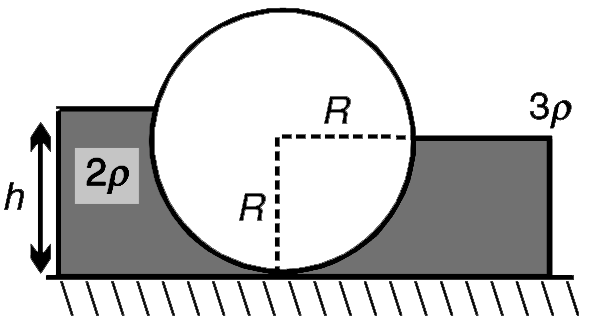
(i) In the figure shown, the heavy cylinder (radius R) resting on a smooth surface separates two liquids of densities 2ρ and 3ρ. Find the height 'h' for the equilibrium of cylinder.
(ii) The cross section of a dam wall is an arc of a circle of radius R=20m subtending on angle of θ=60∘ at the centre of the circle. the centre (O) of the circle lies in the water surface. The width of the dam (i.e., dimension perpendicular to the figure) is b=10m. Neglect atmospheric pressure is following calculations.
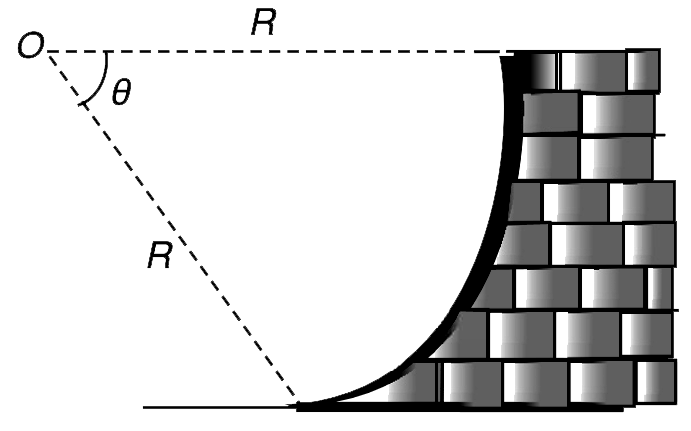
(a) Calculate the vertical component of force (Fx) applied by water on the curved dam wall.
(b) Calculate the horizontal component of force (FH) applied by water on the curved dam wall.
(c) Calculate the resultant force applied by the water on the curved dam wall.
View SolutionIf radius is r and height is h, then find curved surface area of cylinder.
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth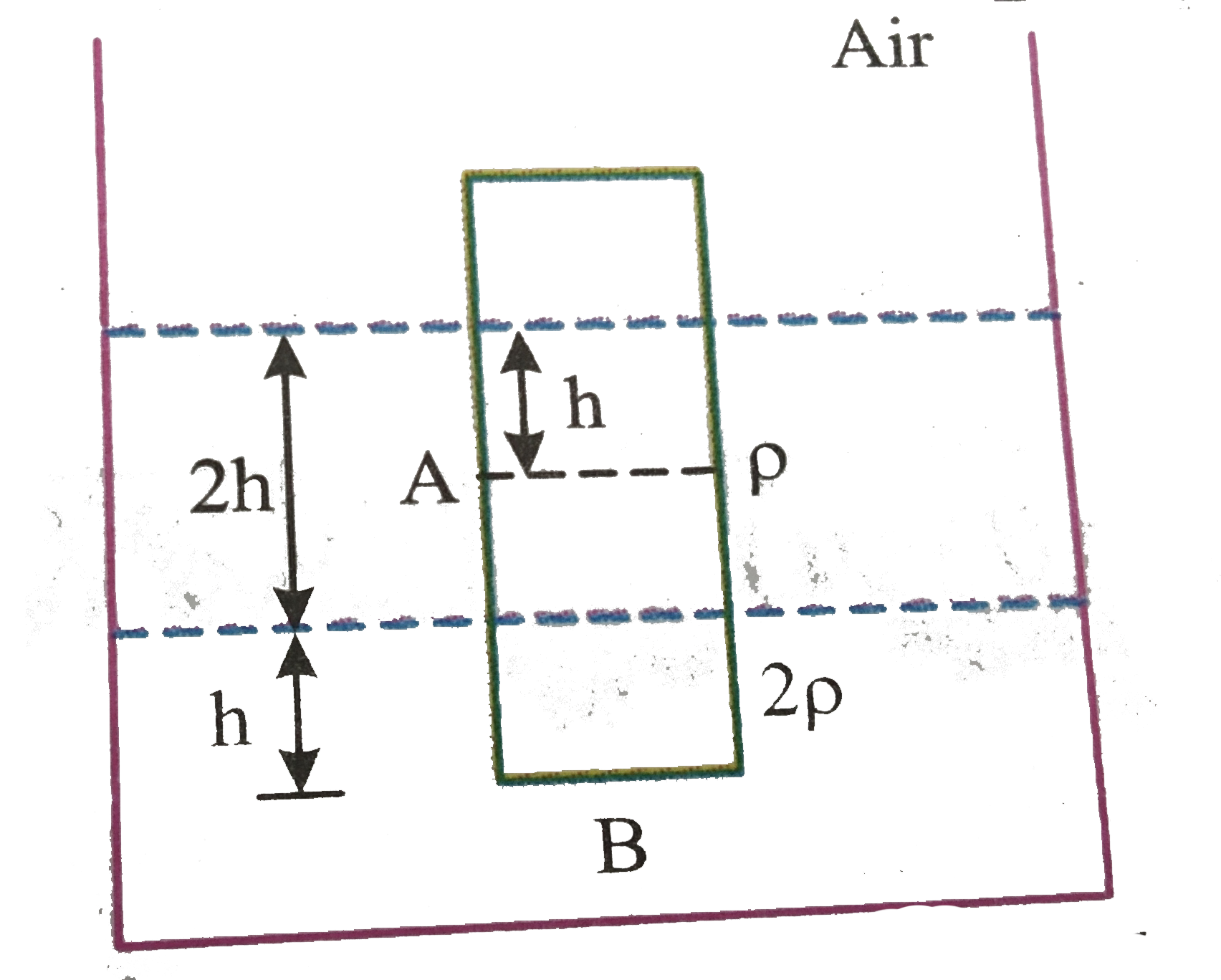
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnoneThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is
 A√6ghB2√ghC2√2ghD√gh
A√6ghB2√ghC2√2ghD√gh
The total surface area of a cylinder of base radius r and height h is______.
View SolutionTwo liquids of densities ρ and 3rho having volumes 3V and V are mixed together. Find density of the mixture.
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
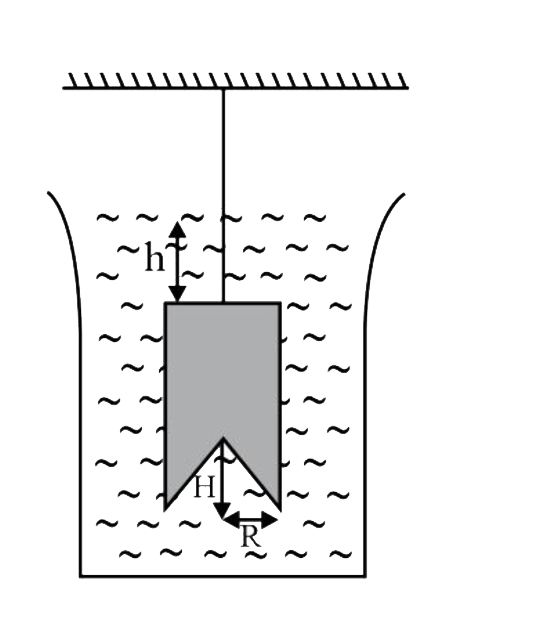
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is

View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
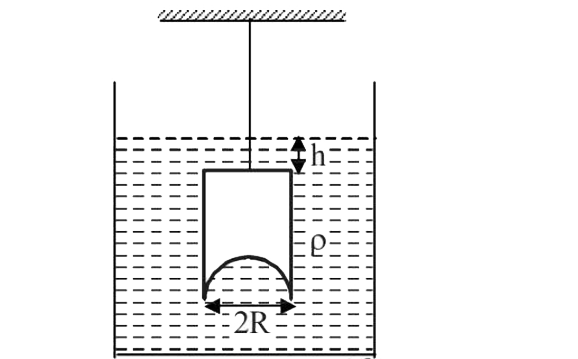
View Solution

