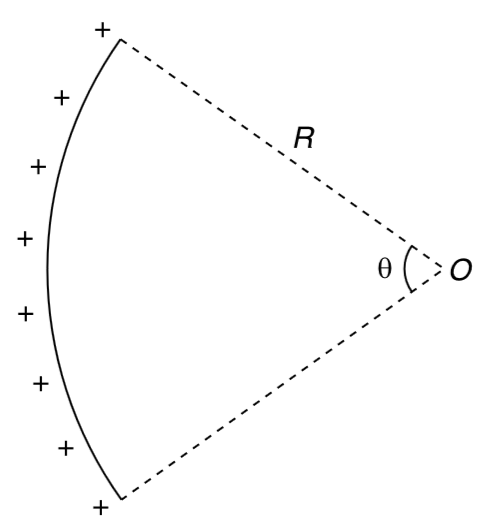
Consider a circular arc of radius $R$ which subtends an angle $ϕ$ at its centre .Let us calculate the electric field strength at $C$

Video Solution

Text Solution

Verified by Experts

Consider a polar segment on arc of angular width $d θ$ at an angle $θ$ from the angular bisector XY as shown. The length of elemental segment is $R d θ$ . The charge on this segment dq is
$d q = \frac{Q}{ϕ} d θ$
Due to this dq, electric field at centre of arc C is given as
$d E = \frac{d q}{4 π ε_{0} R^{2}}$
The electric field component dE to this segment dE $sin θ$ which is perpendicular to the angle bisector gets cancelled out on integration.
The net electric field at centre will be along angle bisector which can be calculate by integrating $d E cos θ$ within limits from $- ϕ / 2$ to $ϕ / 2$
Hence net electric field strength at centre C is
$E_{c} = \int d E cos θ$
$= \int_{- ϕ / 2}^{ϕ / 2} \frac{Q}{4 π ε_{0} ϕ R^{2}} cos θ d θ$
$= \frac{Q}{4 π ε_{0} R^{2} ϕ} \int_{- ϕ / 2}^{ϕ / 2} cos θ d θ$
$= \frac{Q}{4 π ε_{0} R^{2} ϕ} {[sin θ]}_{- ϕ / 2}^{ϕ / 2}$
$\frac{Q}{4 π ε_{0} R^{2} ϕ} [sin ϕ / 2 + sin ϕ / 2]$
$E_{c} = \frac{2 Q sin (ϕ / 2)}{4 π ε_{0} R^{2} ϕ}$
For a semi circular ring $ϕ = π$ . So at centre
$E_{c} = \frac{2 Q sin (ϕ \frac{/}{2})}{4 ε_{0} R^{2} ϕ} = \frac{2 Q sin (π / 2)}{4 π ε_{0} R^{2} π} = \frac{2 Q}{4 π^{2} ε_{0} R^{2}}$

Updated on:21/07/2023

A current $i$ ampere flows in a circular arc of wire whose radius is $R$ , which subtend an angle $3 π / 2$ radian at its centre. The magnetic induction $B$ at the centre is

A $\frac{μ_{0} i}{R}$
B $\frac{μ_{0} i}{2 R}$
C $\frac{2 μ_{0} i}{R}$
D $\frac{3 μ_{0} i}{8 R}$
An are of a circle of a radius R subtends an angle $\frac{π}{2}$ at the centre .it carries a current l. The magnetic field at the centre will be
A $\frac{μ_{0} I}{2 R}$
B $\frac{μ_{0} I}{8 R}$
C $\frac{μ_{0} I}{4 R}$
D $\frac{μ_{0} I}{5 R}$
An arc of a circle of radius $R$ subtends an angle $\frac{π}{2}$ at the centre. It carriers a current $i$ . The magnetic field at the centre will be
A $\frac{μ_{0} i}{2 R}$
B $\frac{μ_{0} i}{8 R}$
C $\frac{μ_{0} i}{4 R}$
D $\frac{2 μ_{0} i}{5 R}$