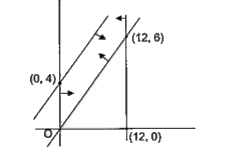
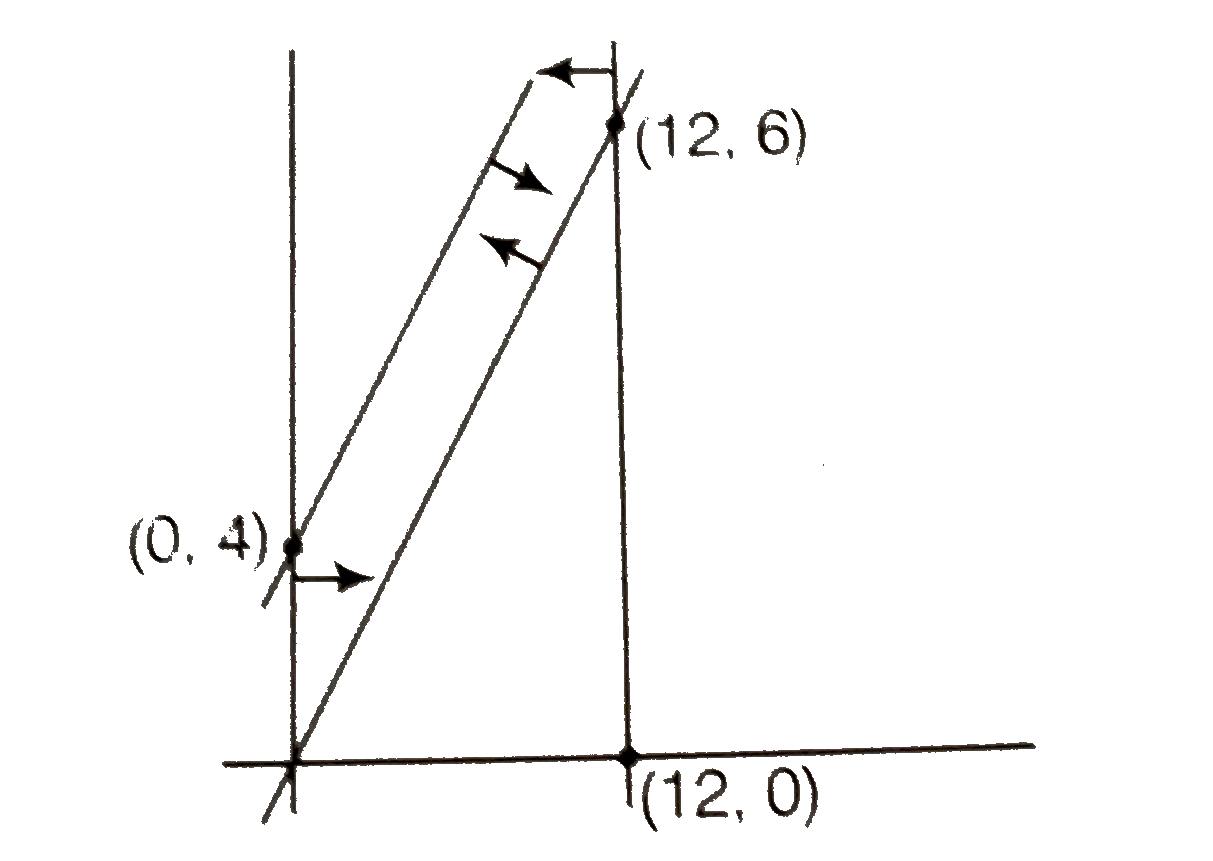
The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
0
8
12
−18
The correct Answer is:C
The feasible region as shown in the region has objective funciton F=3x-4y.

Hence, the maximum value of F is 12.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
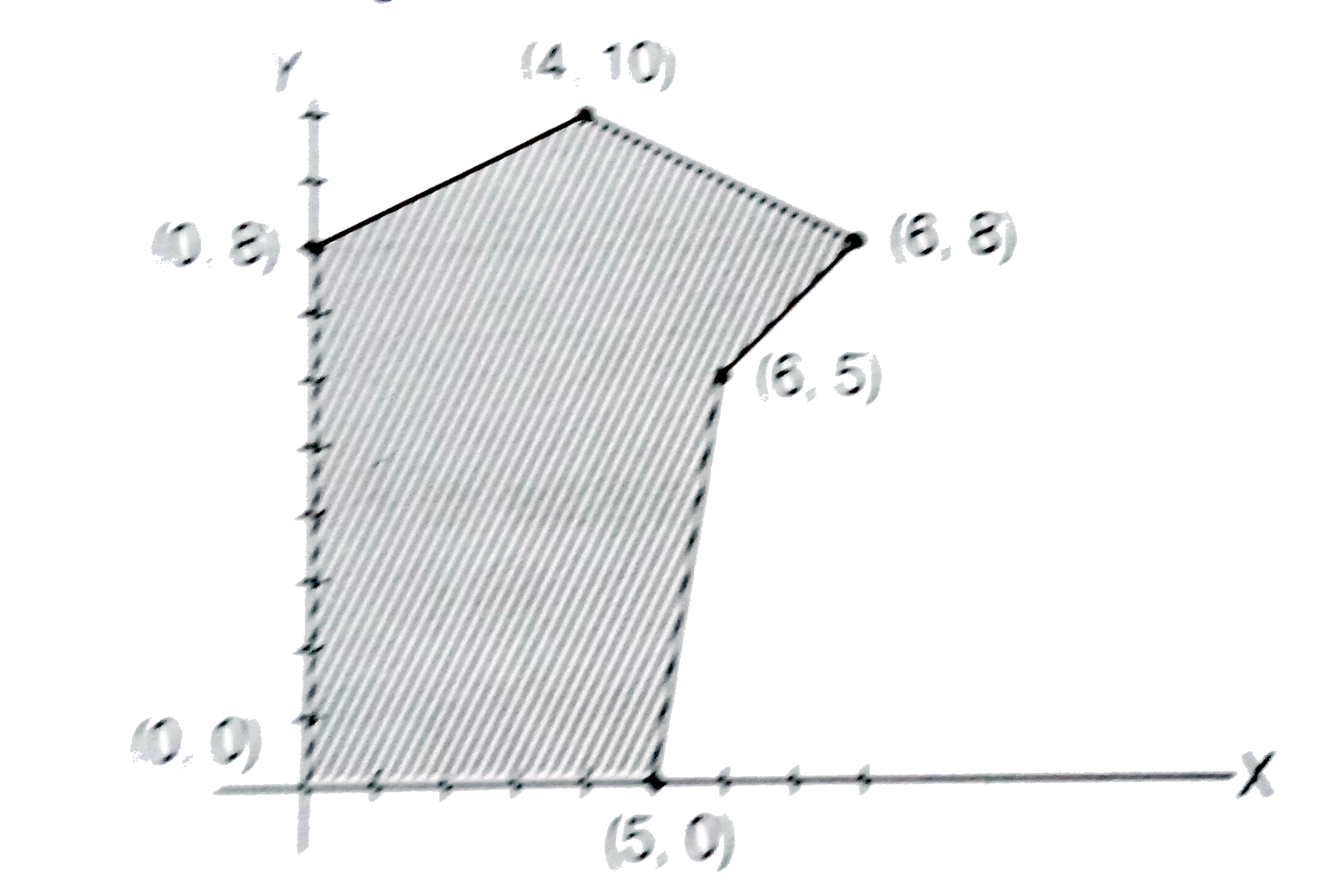 A(0,0)B(0,8)C(5,0)D(4,10)
A(0,0)B(0,8)C(5,0)D(4,10)The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
A22B23C24D21
The feasible solution for a LPP is hown as below,

Let Z =3x -4y be the objective function . Then,
Maximum of Z occurs at
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

View SolutionThe feasible solution for a LPP is hown as below,
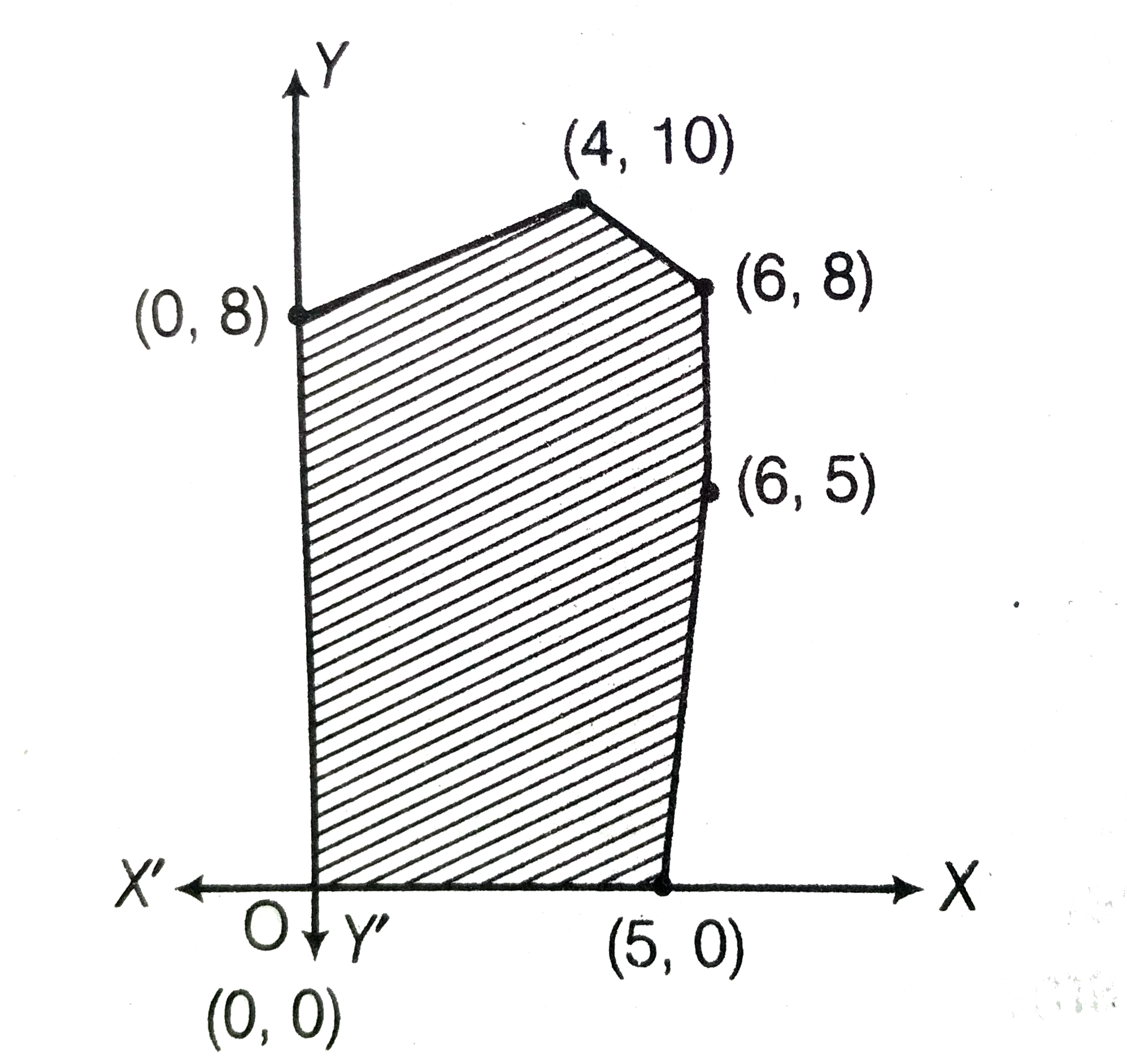
Let Z =3x -4y be the objective function . Then, Minimum of Z occurs at
View SolutionThe feasible region of an LPP is shown in the figure. If z=3x+9y ,then the minimum value of z occurs at
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:

View Solution