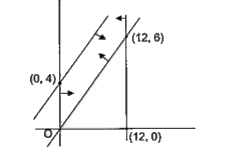
The feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

Video Solution
Text Solution
The correct Answer is:N/a
From the shaded region, it is clear that feasible region is unbouded with the corner points A (4,0), B(2,1), and C(0,3)
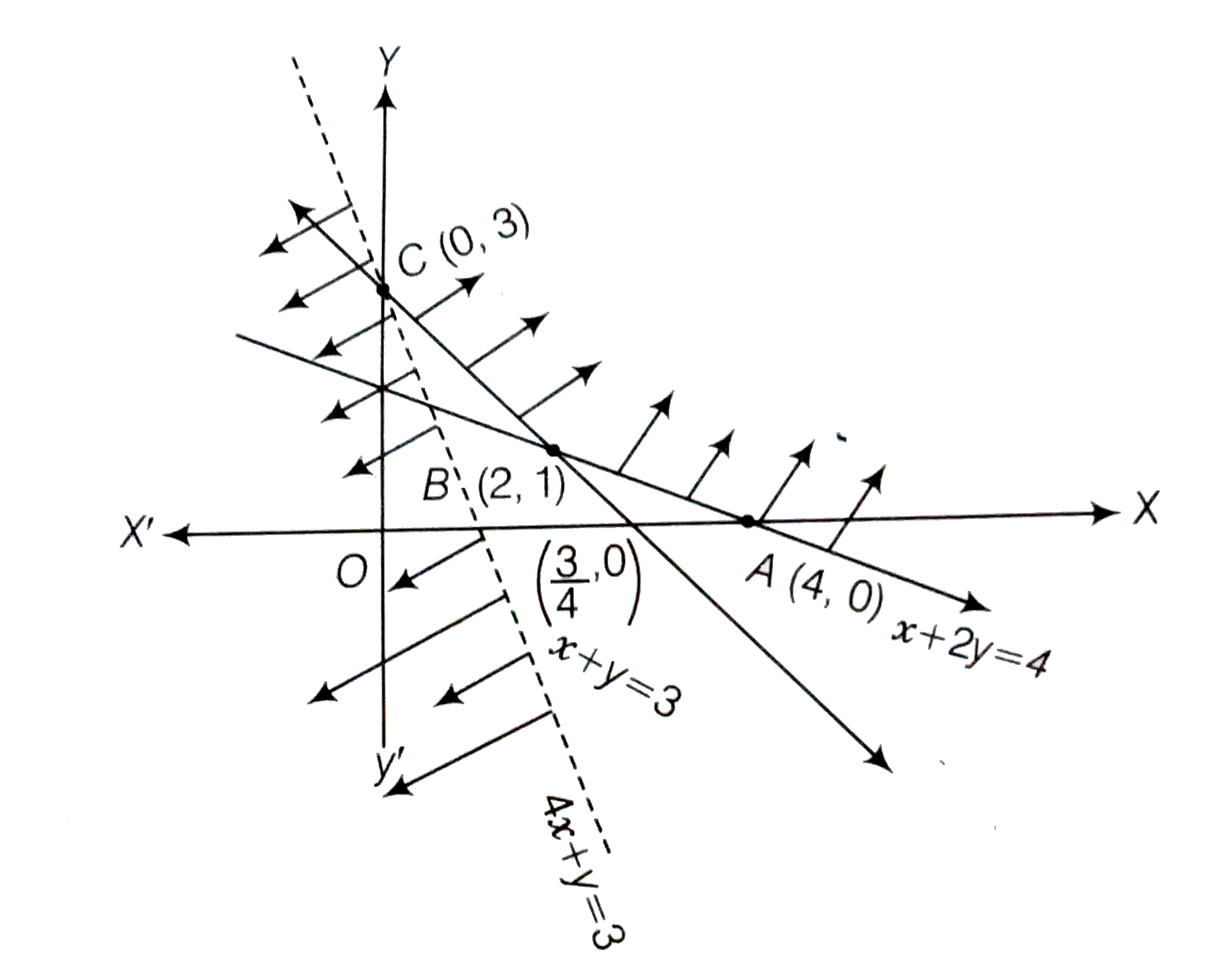
Now we see that 3 is the smallest value of Z at the corner point (0,3). Note that here we see that the region is unbounded, therefore 3 may or may not be the minimum value of Z. To decided this issue, we graph the inequality 4x+y≤3 and check whether ther resulting open half plan has not point in common with feasible reigon otherwise, Z has no minimum value. From the shown graph above,it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0,3)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
A22B23C24D21The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
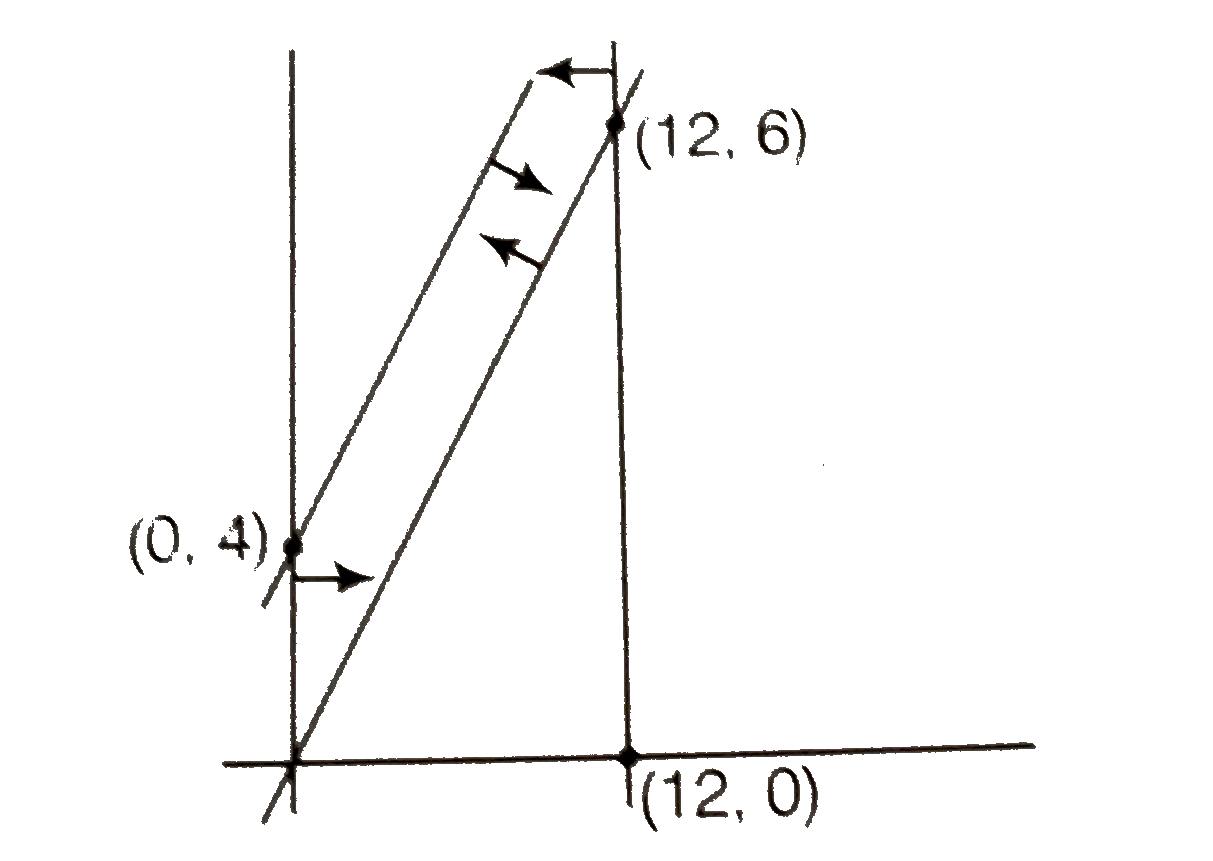 A0B8C12D−18
A0B8C12D−18The feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
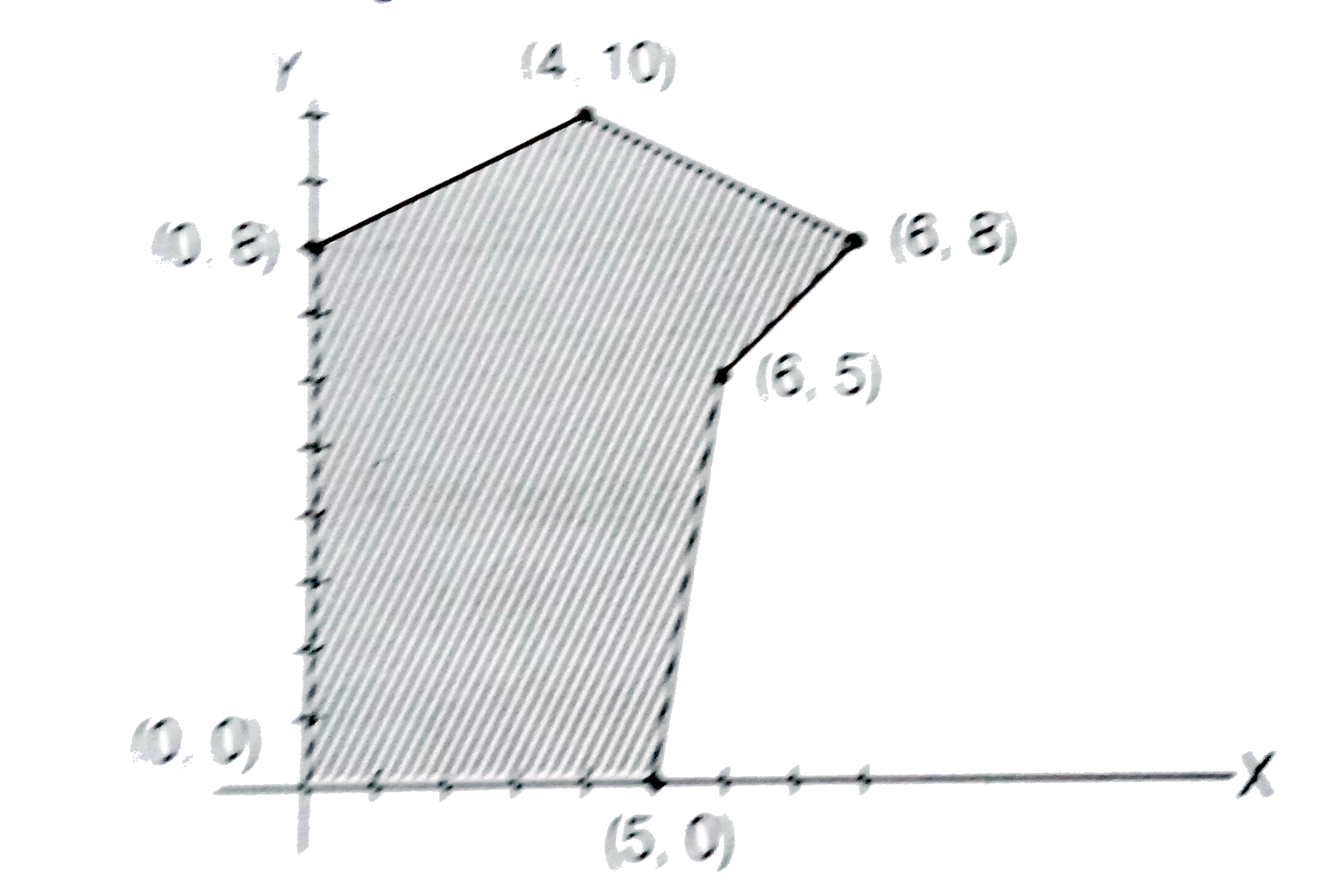 A(0,0)B(0,8)C(5,0)D(4,10)
A(0,0)B(0,8)C(5,0)D(4,10)
Find x,y and z in each of the following figure:

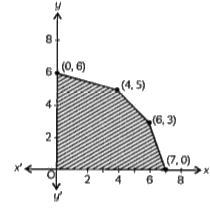
View SolutionThe feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
View SolutionFind the minimum value of ∣z−1 if ||z−3|−|z+1∣∣=2.
View SolutionThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:

View SolutionThe feasible region for an LPP is shown in the below. Let F = 3x - 4y be the objective function. Maximum value of F is :
View Solution


