In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
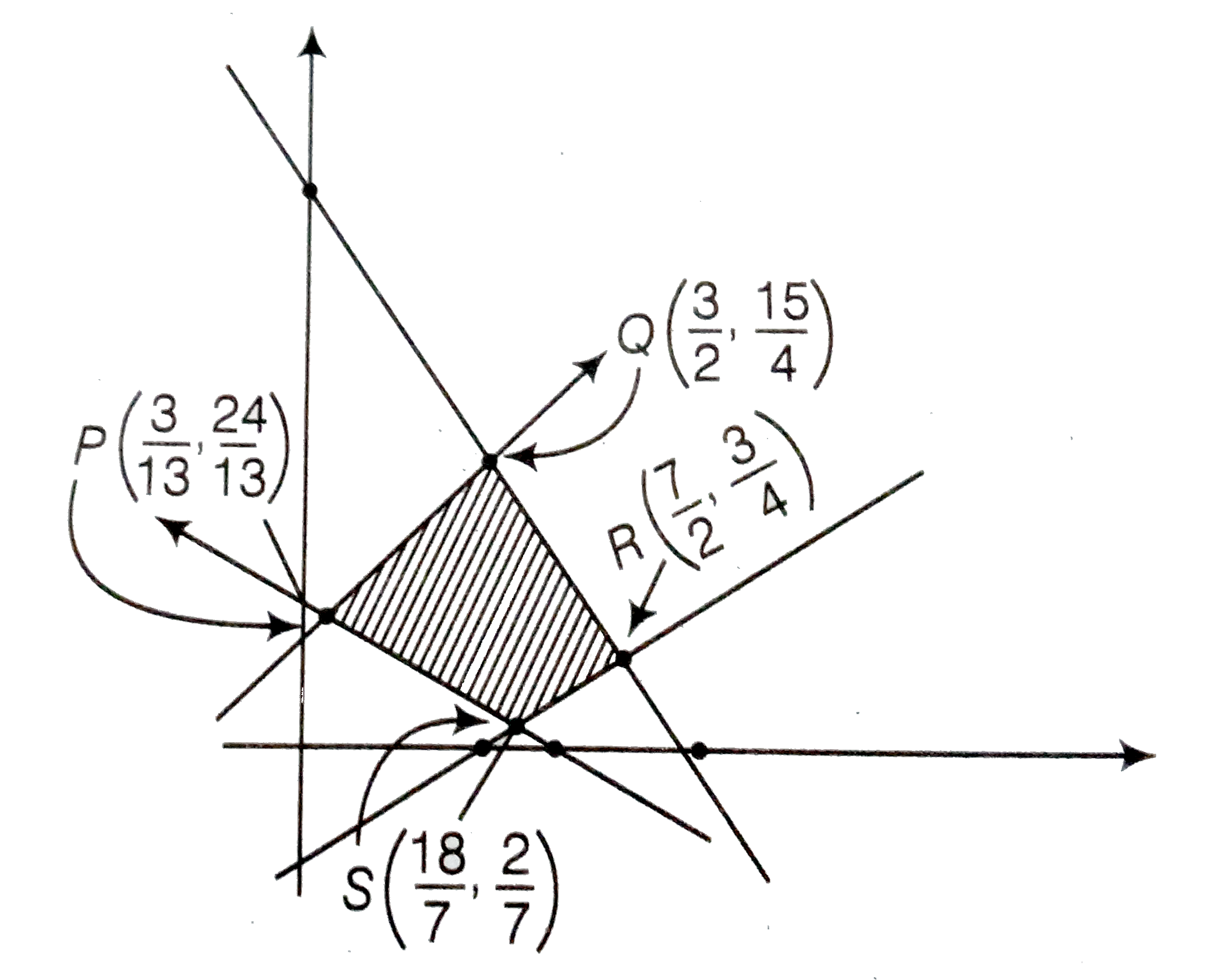
A
maximum = 7 minimum = 479
B
maximum = 9 minimum = 317
C
maximum = 10 minimum = 345
D
maximum = 8 minimum = 547
Video Solution
Text Solution
The correct Answer is:B
From the shaded bounded region. It is clear the coordinates of corner points are
(313,2413),(187,27),(72,34)and(32,154)
Also we have to determine maximum and minimum value of Z=x+2y.
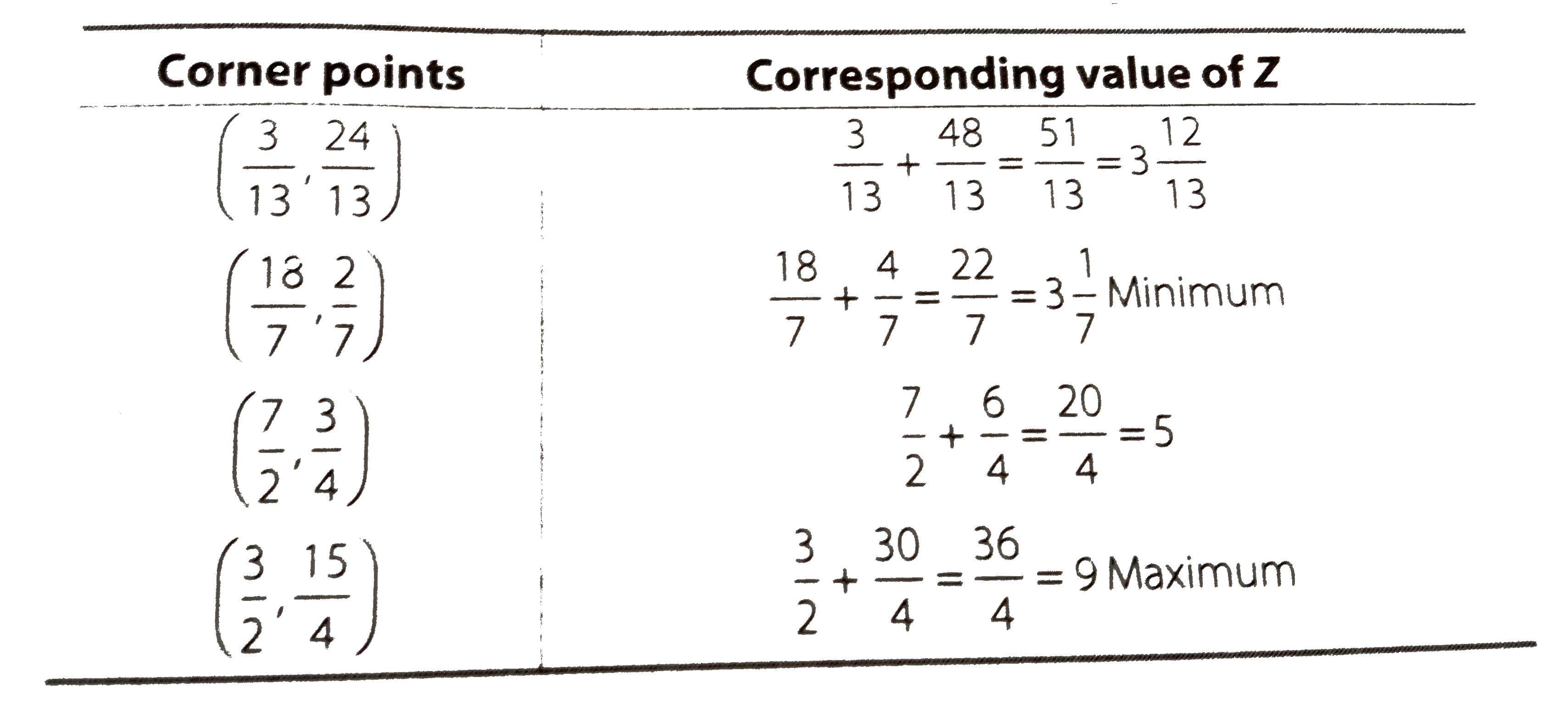
Hence, the maximum and minimum value of Z are 9 and 317, respectively
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
A22B23C24D21The corner point method for bounded feasible region comprises of the following steps
I. When the feasible region is bounded, M and m are the maximum and minimum values of Z.
II. Find the feasible region of the linear programming problem and determine its corner points.
Ill. Evaluate the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values of these points.
The correct order of these above steps isAIII,I,IIBII,III,ICII,I,IIIDI,III,IIConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IV
If ∣∣∣z+4z∣∣∣=2, find the maximum and minimum values of |z|.
View SolutionState True or False:
If the corner points of the feasible region are (0, 10),(2, 2) & (4, 0) then the minimum value of Z = 3x + 2y is at (4, 0)
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
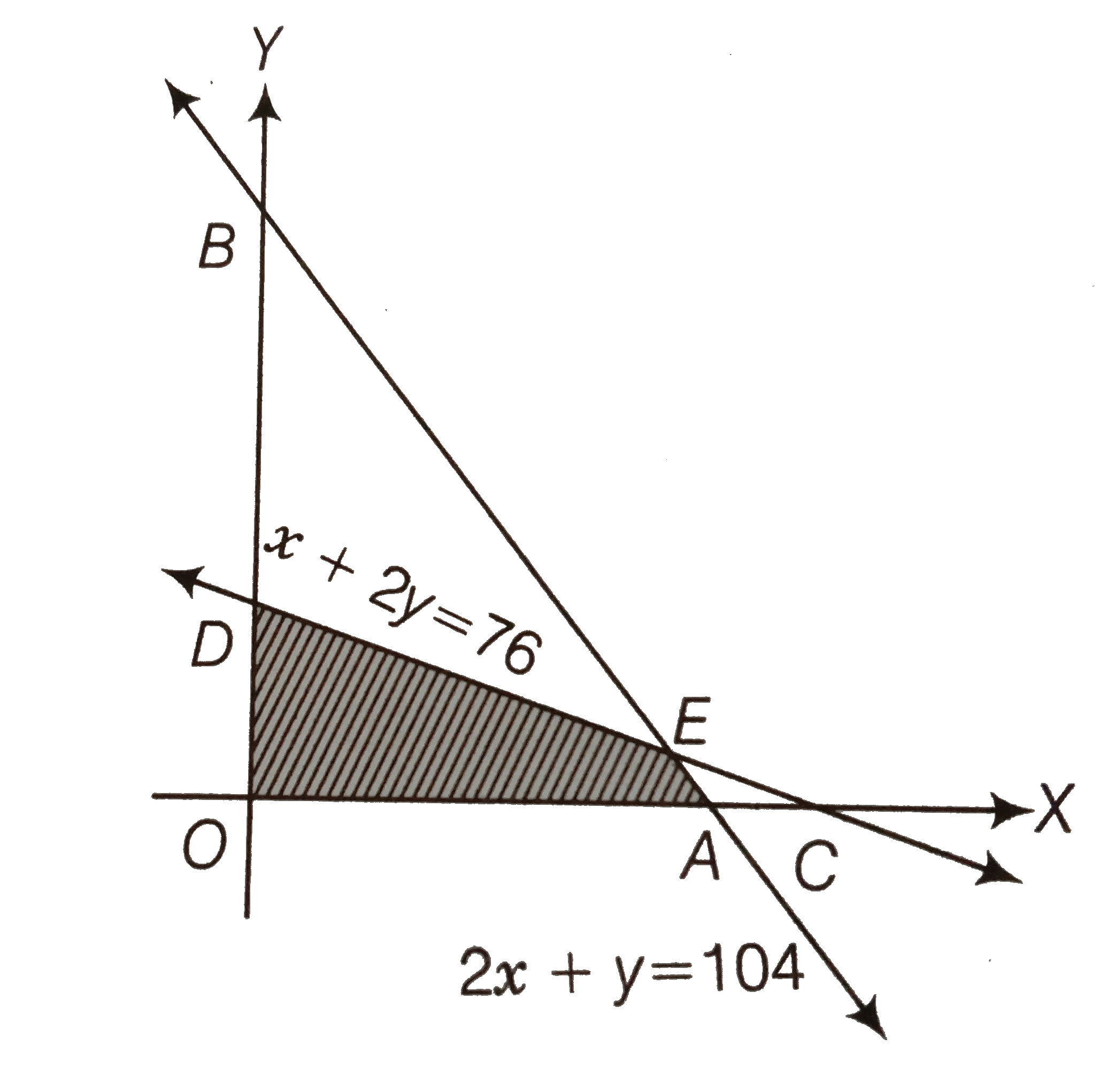
View SolutionState True or False:
If the corner points of the feasible region are (0, 7/3),(2,1),(3, 0) & (0,0) then the maximum value of Z = 4x + 5y is 12 .
View SolutionLet R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
View Solution

