The corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
The quantity in Column A is greater
The quantity in column B is greater
The two quantities are equal.
The relationship cannot be determined on the basis of the information supplied.
The correct Answer is:B

Hence, maximum value of Z=300<325
So, the quantity in column B is greater.
Topper's Solved these Questions
Similar Questions
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40). (20, 40), (60, 20). (60, 0). "The objective function is Z=4x+3y.
Compare the quantity in Column A and Column B.
Column AColumn BMaximum of Z325
View SolutionThe corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View Solution
Knowledge Check
The corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
A5p = 2qB2p=5qCp = 2qDq = 3pThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
Ap=qBp=2qCq=2pDq=3pThe carner points of the feasible region formed by the system of linear inequations x−y≥−1,−x+y≥0,x+y≤2andx,y≥0, are
A(0,0),(−1,0),(0,1)B(0,0),(2,0),(1,1)C(0,1),(1,1),(0,0)D(0,0),(1,1),(12,32),(0,1)
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
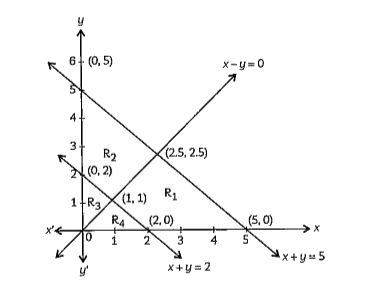
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
View SolutionThe corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
View SolutionIf the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
View Solution

