If the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
Video Solution
Text Solution
The correct Answer is:1
N/a
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IV
Z may not be:ACH3−ClBCH3H∣C∣CH3−ClC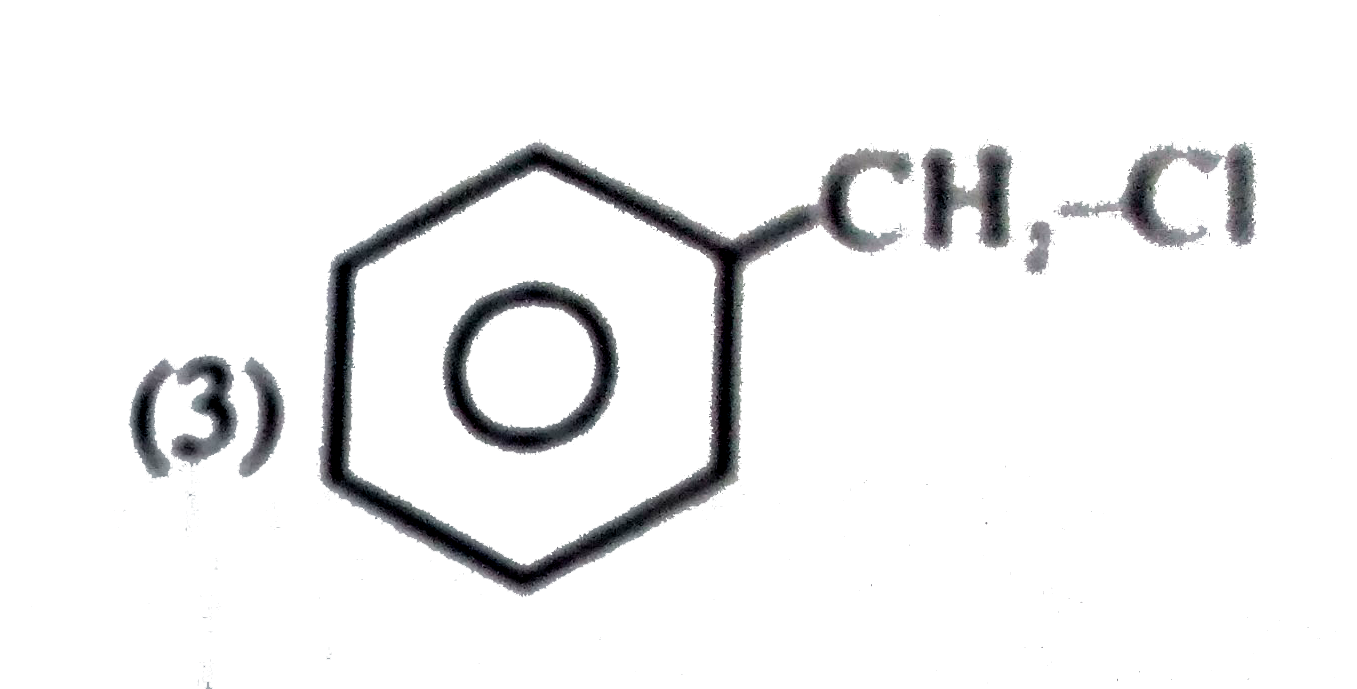 D
D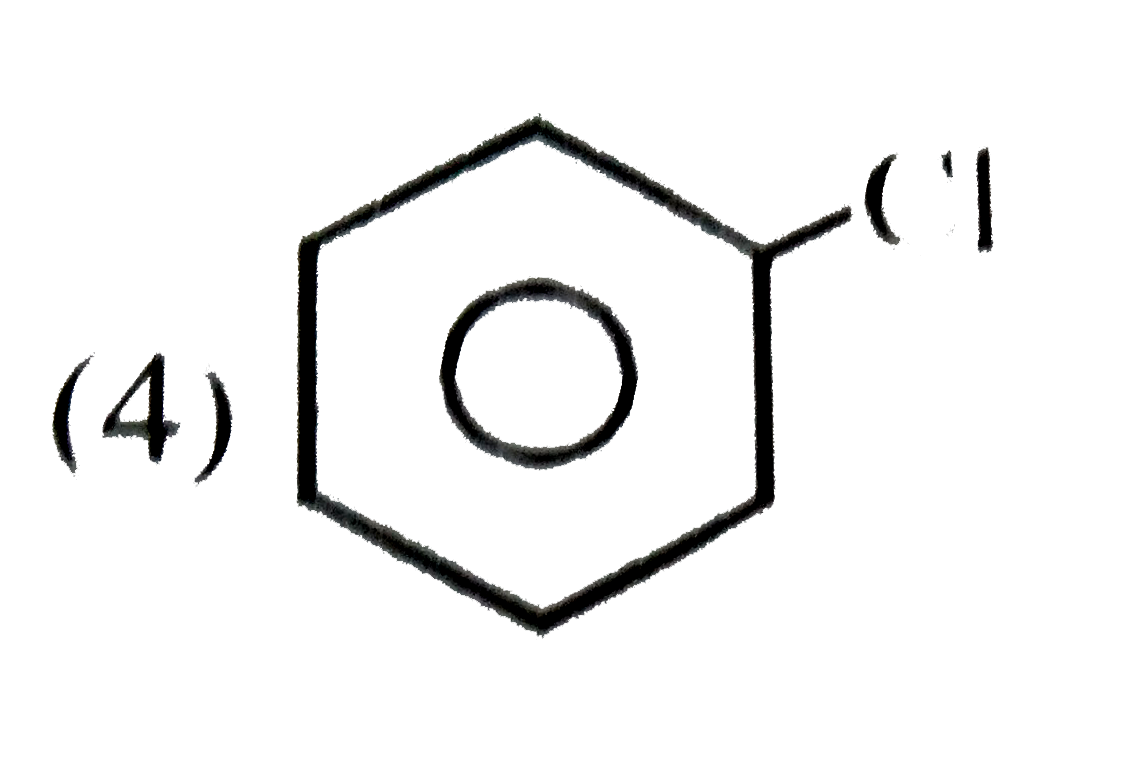
Objective function of an LPP is
Aa constraintBa function to be optimisedCa relation between the variablesDnone of the above
In a LPP, the objective function is always.
View SolutionThe feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
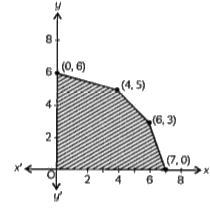
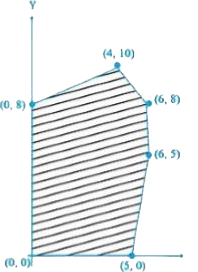
View SolutionIn the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
View SolutionLet R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
View SolutionWhich of the following statements is false?
View Solution

