Let R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false? A) When Z has an optimal value, where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region . B)If R is bounded, then the objective function Z has both a maximum and a minimum value on Rand each of these occurs at a corner point of R . C) If R is unbounded, then a maximum or a minimum value of the objective function may not exist D) If R is unbounded and a maximum or a minimum value of the objective function z exists, it must occur at corner point of R
When Z has an optimal value, where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region .
If R is bounded, then the objective function Z has both a maximum and a minimum value on Rand each of these occurs at a corner point of R .
If R is unbounded, then a maximum or a minimum value of the objective function may not exist
If R is unbounded and a maxil'TUJm or a minimum value of the objective function z exists, it must occur at corner point of R
The correct Answer is:D
If the feasible region is unbounded and the maximum or a minimum value of Z exists, it must occur at a corner point of R.
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
One of the corner points of the feasible region of inequalities gives
AOptimal solution of LPPBObjective functionCConstraintsDLinear assumptionsThe optimal value of the objective function is attained at the points
Agiven by intersectionn of inequations with axis onlyBgiven by intersection of inequations with X-axis onlyCgiven by corner points of the feasible regionDnone of the aboveThe optimal value of the objective function is attained at the points
Agiven by intersectionn of inequations with axis onlyBgiven by intersection of inequations with X-axis onlyCgiven by corner points of the feasible regionDnone of the above
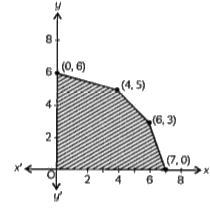
In the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
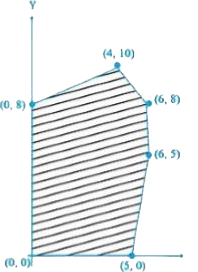
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
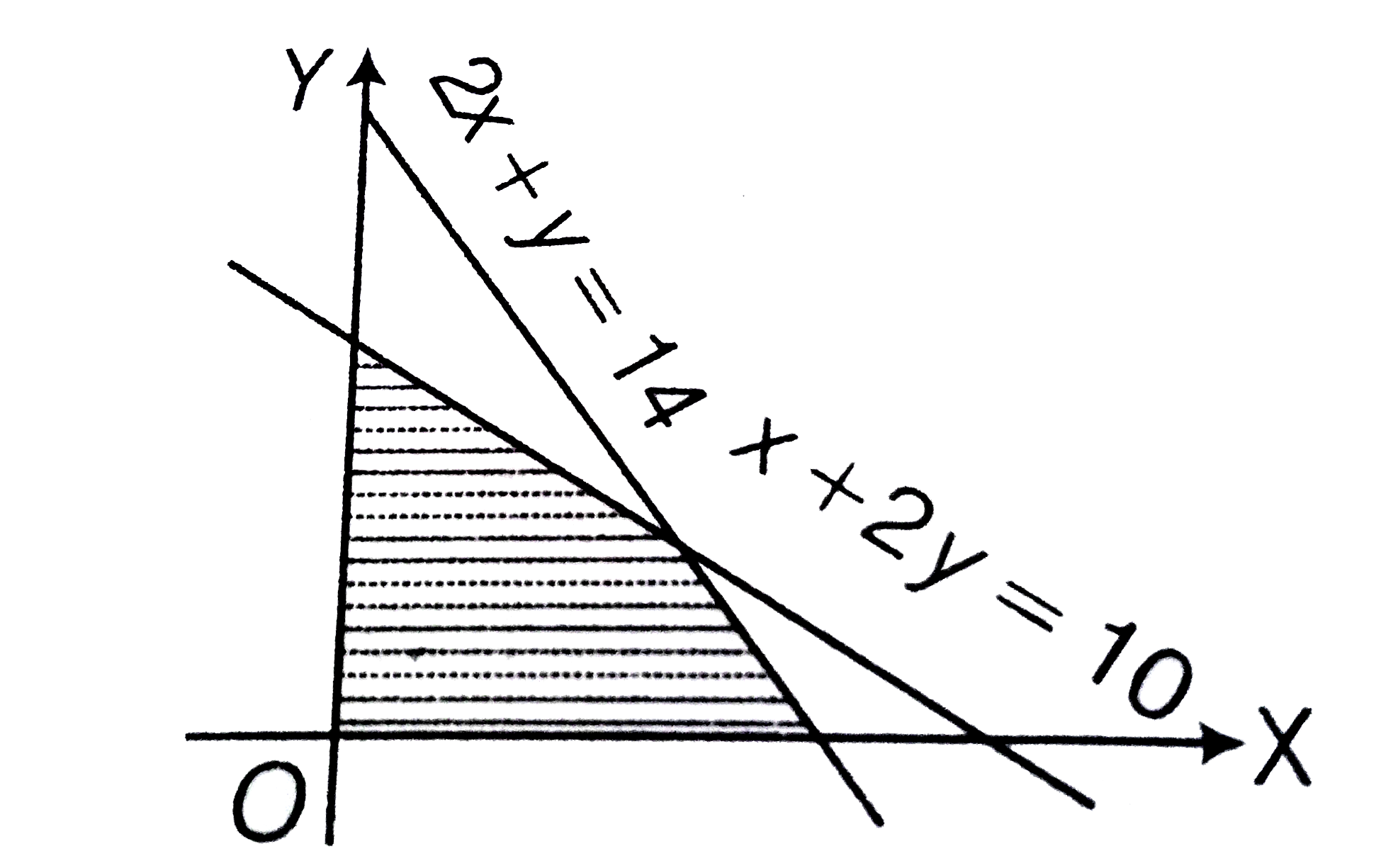
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
View SolutionVariables of the objective function of the linear programming problem are
View SolutionIn case of a linear programming problem, feasible region is always
View Solution