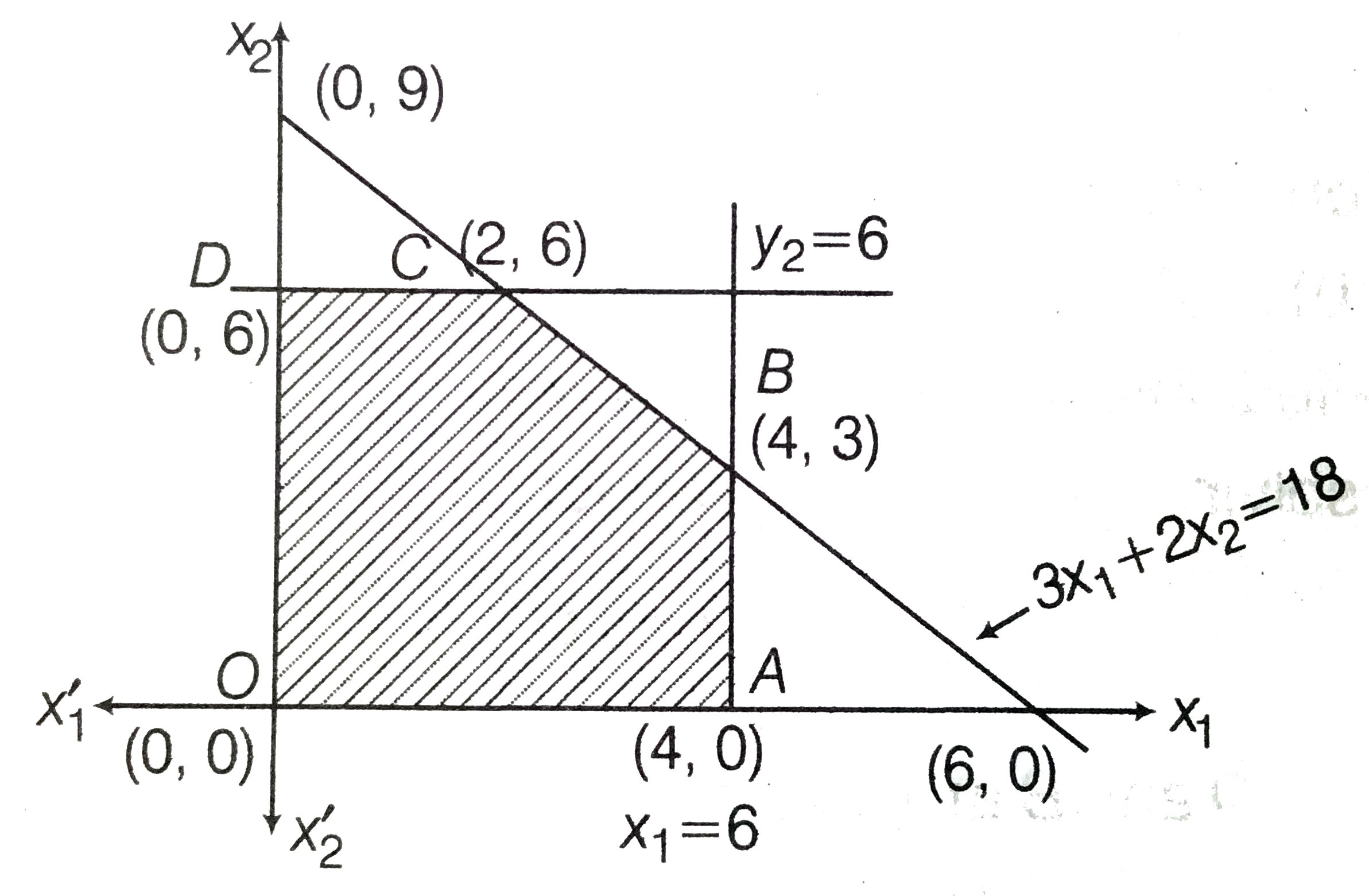
By graphical method, the solutions of linear programming problem maximum $Z = 3 x_{1} + 5 x_{2}$ subject to constraints $3 x_{1} + 2 x_{2} \leq 18$
$x_{1} \leq 4, x_{2} \leq 6, x_{1} \geq 0, x_{2} \geq 0$

A

$x_{1} = 2, x_{2} = 6, Z = 36$

B

$x_{1} = 2, x_{2} = 6, Z = 36$

C

$x_{1} = 4, x_{2} = 3, Z = 27$

D

$x_{1} = 4, x_{2} = 6, Z = 42$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The feasible region is OABCDO, whose corner points are O (0, 0), A ( 4, O), B ( 4, 3), C (2, 6) and D (0, 6). :. Table for objective function is given as: $∴$ Table for objective function is given as:

Hence, maximum values of Z is 36 at point C(2, 6). So, $x_{1} = 2, x_{2}$ =6andZ=36

|

Updated on:21/07/2023

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
By graphical method, the solutions of linear programming problem maximise $Z = 3 x_{1} + 5 x_{2}$ subject to constraints $3 x_{1} + 2 x_{2} \leq 18, x_{1} \leq 4, x_{2} \leq 6 x_{1} \geq 0, x_{2} \geq 0$ are
A $x_{1} = 2, x_{2} = 0, Z = 6$
B $x_{1} = 2, x_{2} = 6, Z = 36$
C $x_{1} = 4, x_{2} = 3, Z = 27$
D $x_{1} = 4, x_{2} = 6, Z = 42$
Question 2 - Select One
The iinear programming problem Maximise $Z = x_{1} + x_{2}$
Subject to constraints
$x_{1} + 2 x_{2} \leq \leq 2000$
$x_{1} + x_{2} \leq 15000$
$x_{2} \leq 600$
$x_{1} \geq h a s$
Ano feasible solution
Bunique optimal solution
Ca finite number of optimal solutions
Dinfinite number of optimal solutions
Question 3 - Select One
Solve the linear programming problem. Maximise Z = x + 2y
Subject to constraints $x - y \leq 10, 2 x + 3 y \leq 20$ and $x \geq 0, y \geq 0$
AZ=10
BZ=30
CZ=40
DNone of these

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-Linear Programming -EXERCISE 2 (MISCELLANEOUS PROBLEMS )

Home
Ask Doubt
Profile