Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
A
I and IV
B
II and III
C
I and III
D
II and IV
Video Solution
Text Solution
The correct Answer is:A
Maximum value of the objective function Z =ax+ by in an LPP may occur at more than one corner points.
∴ Statement II is false Also, in an LPP, since both x and y cannot be zero simultaneously. ∴ Minimum value of the objective function Z = ax + by cannot be 0, if origin is one of the corner point of the feasible solution.
∴ Statement Ill is false.
If the feasible region for LPP is unbounded, then maximum or minimum of the objective function Z = ax + by may or may not exist, statement I is correct.
Also, in an LPP the maximum value of the objective function Z = ax + by is always finite.
|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
Objective function of an LPP is
Aa constraintBa function to be optimisedCa relation between the variablesDnone of the aboveIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
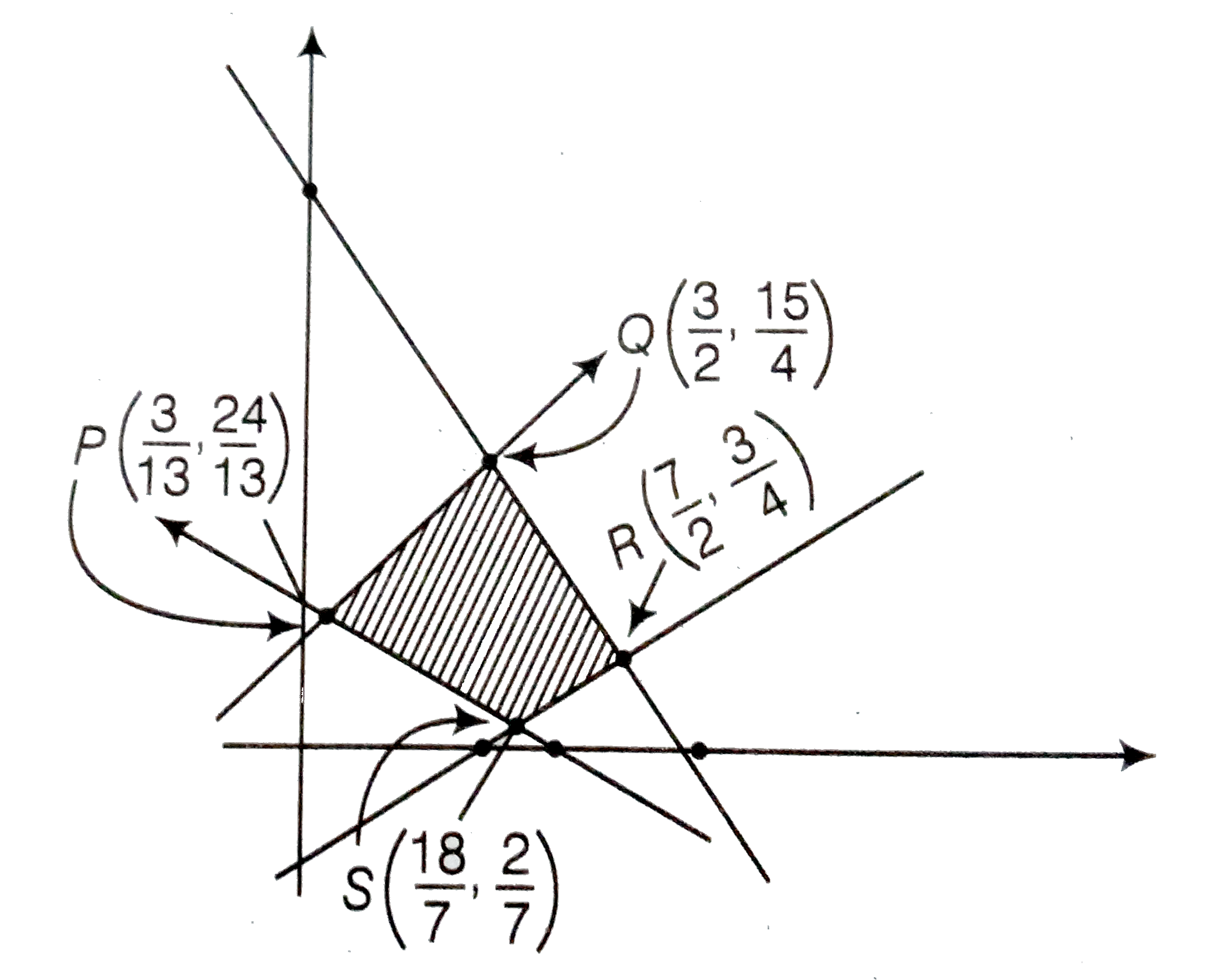 Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547
Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547The corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:
A20B23C27D18
In a LPP, the maximum value of the objective function Z = ax +by is always finite.
View SolutionIf the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionDefine a corner point of a feasible region.
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionIn a LPP, the objective function is always.
View Solution
