The minimum and maximum values problem, of Z for the minimise and maximise Z = 3x + 9 y subject to the constraints
x+3y≤60,x+y≥10,x≤y,
are respectively
A
60 and 180
B
180 and 60
C
50 and 190
D
190 and 50
Video Solution
Text Solution
The correct Answer is:A
Given Z= 3x+9y
Subject to the constraints
x+3y≤60
x+y≥10
x≤y
and x≥0,y≥0
The feasible region is ABCD whose corner points A,B,C and D are (0,15),(5,5),(15,5) and (0,20) respectively .
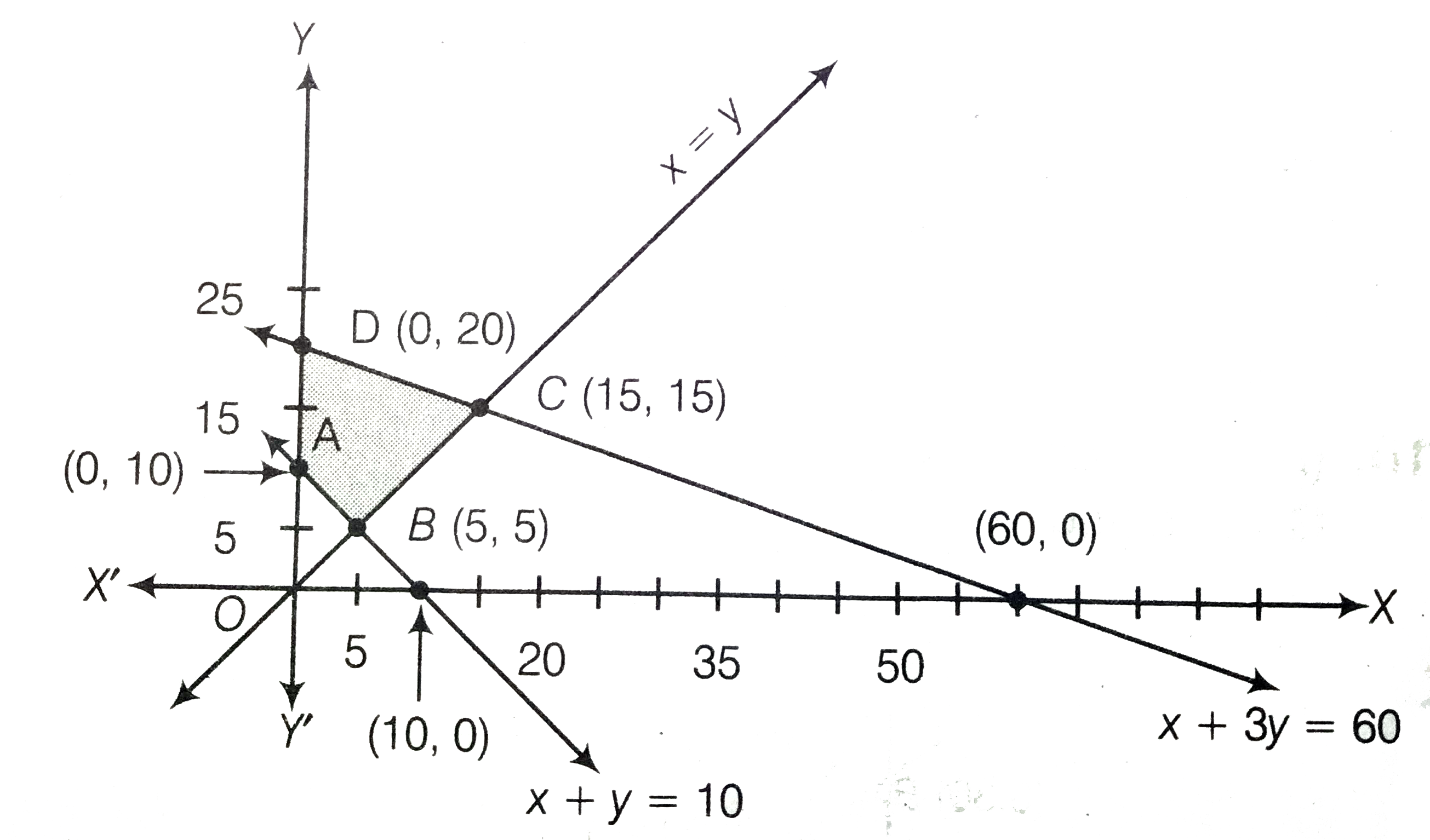
Form the table, the minimum value of Z is 60 and the maximum value of Z is 180.
|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )
15 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
The maximum value of Z = 4x + 2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
A20B36C40DNone of these
Maximize Z=5x+3y subject to the constraints: 3x+5y≤15,5x+2y≤10,x≥0,y≥0
View SolutionMinimize Z=3x+2y subject to the constraints : x+y≥8,3x+5y≤15,x≥0,y≥0.
View SolutionMaximize z=5x+10y subject to constraints x+2y≤10,3x+y≤12,x≥0,y≥0
View SolutionMaximize z=7x+11y subject to the constraints 3x+5y≤26,5x+3y≤30,x≥0,y≥0
View SolutionMaximize z=2x+3y subject to constraints x+4y≤8,3x+2y≤14,x≥0,y≥0.
View SolutionMinimize Z=−3x+4y subject ot constraints : x+2y≤8,3x+2y≤12,x≥0,y≥0.
View SolutionFind maximum value of z=2x+3y subject to the constraints x+y≤4,x≥0,y≥0 .
View Solution
