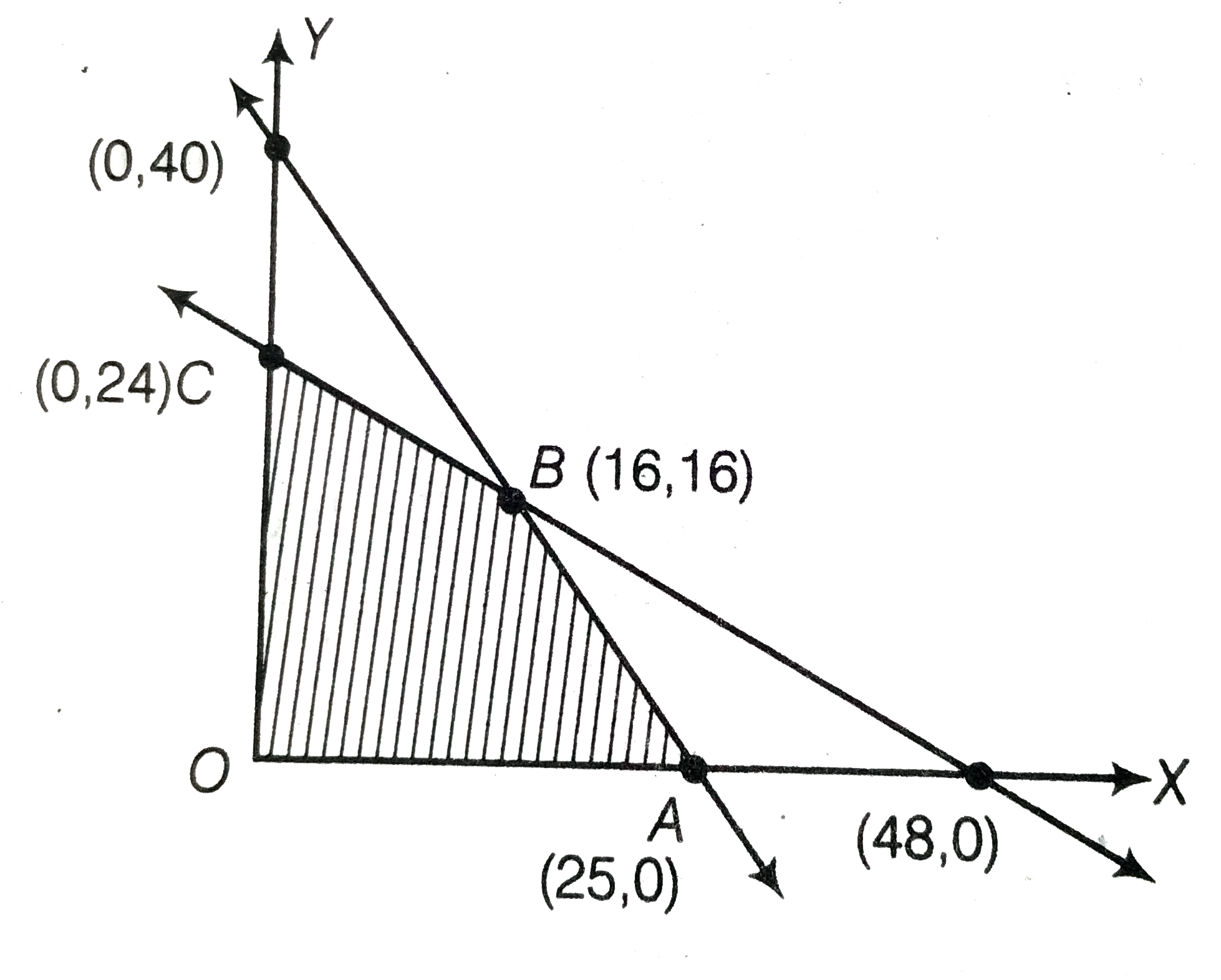
Determine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
The correct Answer is:N/a
As clear from the graph, corner points are O, A, E and D with corrdingates (0,0),(52,0),(144,16) and (0,38) respectively, Also, given region is bounded
Here, Z=3x+4y
∴2x+y=104and2x+4y=152
⇒−3y=−48
⇒y=16andx=44

Hence, Z is at (44,16) is maximum value is 196
Topper's Solved these Questions
Similar Questions
Knowledge Check
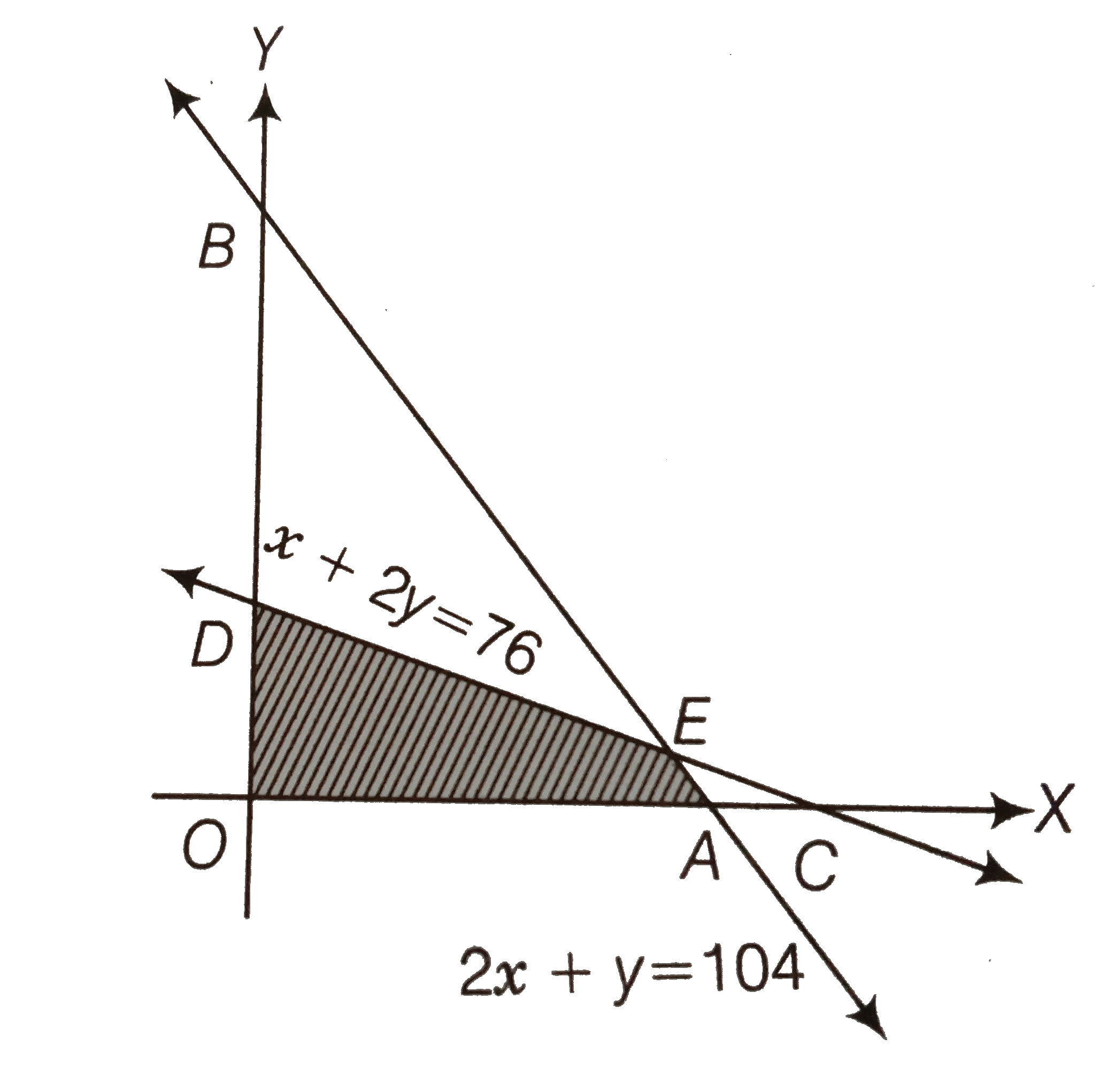
Determine the minimum value of Z=3x+2y (if any), if the feasible region for an LPP is shown in figure:
 AMinimum value of Z = 11.BMinimum value of Z = 14.CMinimum value of Z = 12.DMinimum value of Z = 13.
AMinimum value of Z = 11.BMinimum value of Z = 14.CMinimum value of Z = 12.DMinimum value of Z = 13.The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
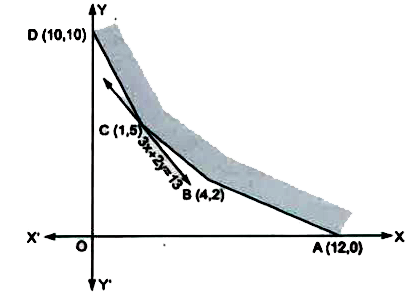
A22B23C24D21In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
 Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547
Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547
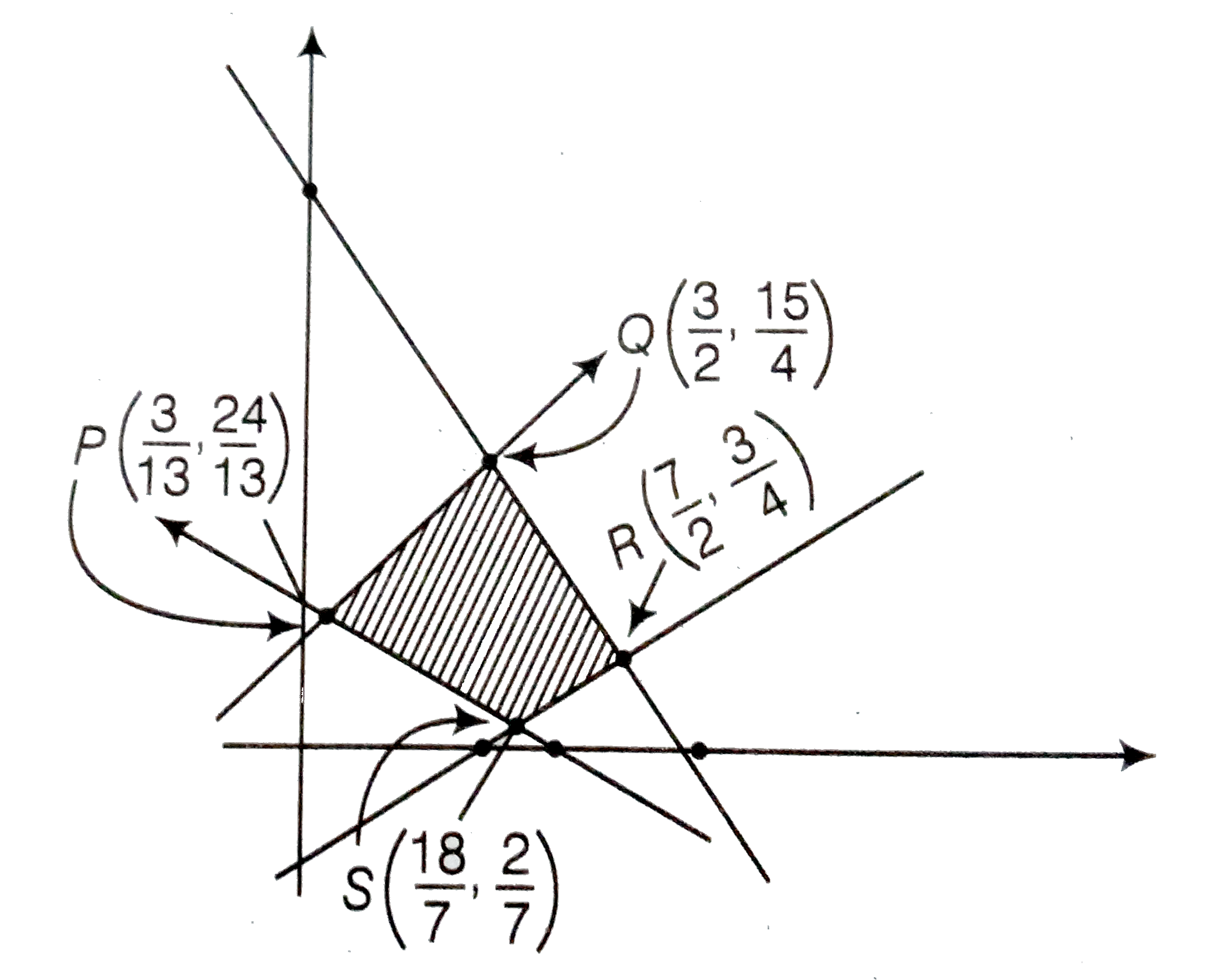
Find the maximum value of f(x,y)=3x+8y in following feasible region:
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
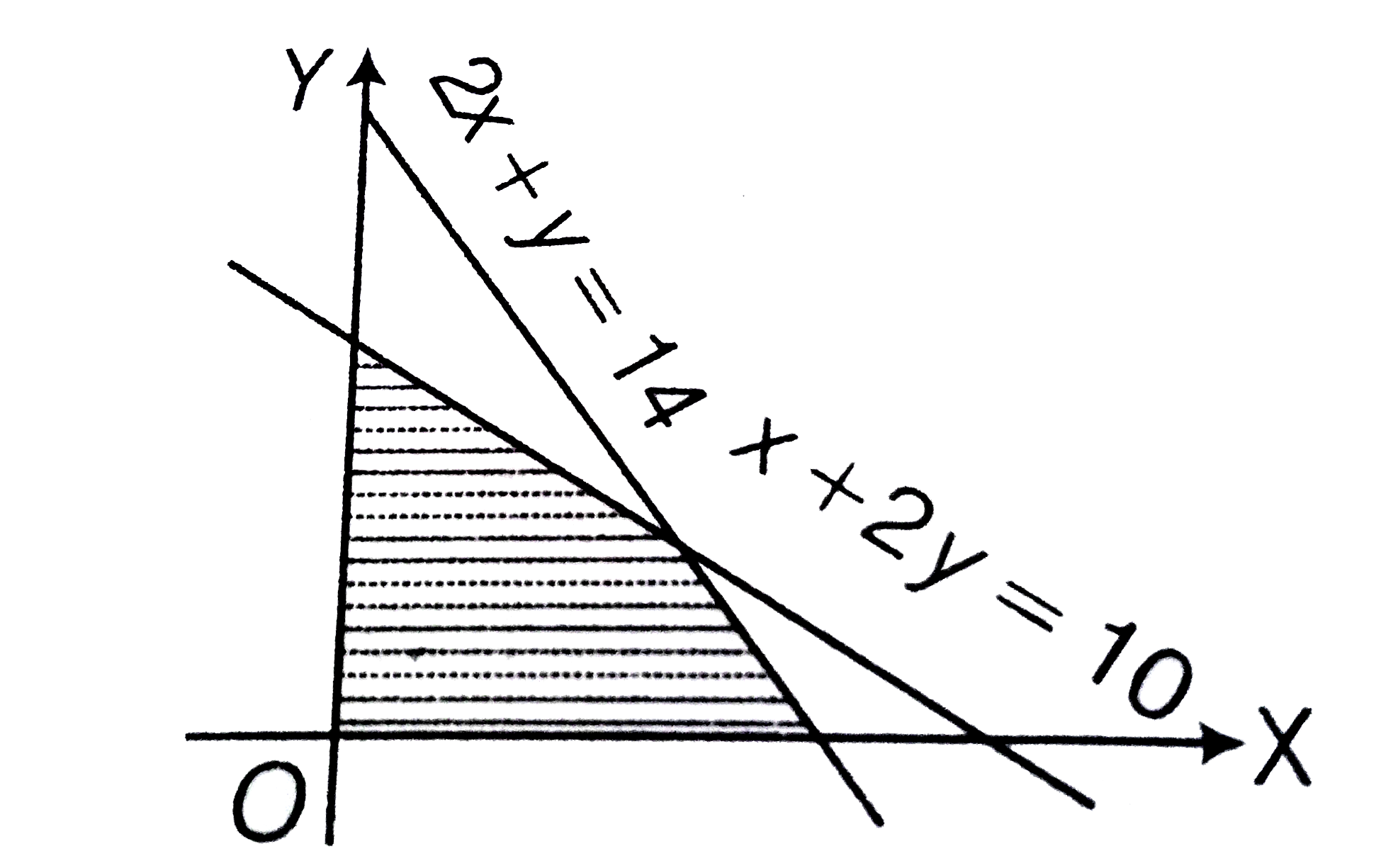
View SolutionThe maximum value of objective function Z=3x+y under given feasible region is
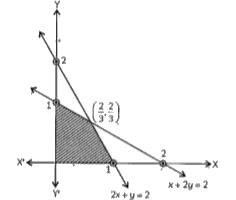
View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View SolutionLet the feasible region of the linear programming problem with the objective function Z = ax + by is unbounded and let M and m be the maximum and minimum value of Z, respectively. Now, consider the following statements
I. M is the maximum value of Z, if the open half plane determined by ax + by gt M has no point in common with the feasible region. Otherwise, Z has no maximum value.
II. mis the minimum value of Z, if the open half plane determined by ax + by lt m has no point in common with the feasible region. Otherwise, Z has no minimum value. Choose the correct option.
View Solution