The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

A
22
B
23
C
24
D
21
Video Solution
Text Solution
The correct Answer is:D
From the figure, it is clear that feasible region is bounded with corrdinates of corner points as (0,3),(3,2) and (0,5). Here Z=11x+7y.
∴x+3y=9andx+y=5
⇒2y=4
∴y=2andx=3
So, intersection points of x+y=5 and x+3y=9 is (3,2)

Hence, the minimum value of Z is 21 at (0,3)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the minimum value of |x−3|+11
A8B11C0D−8In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
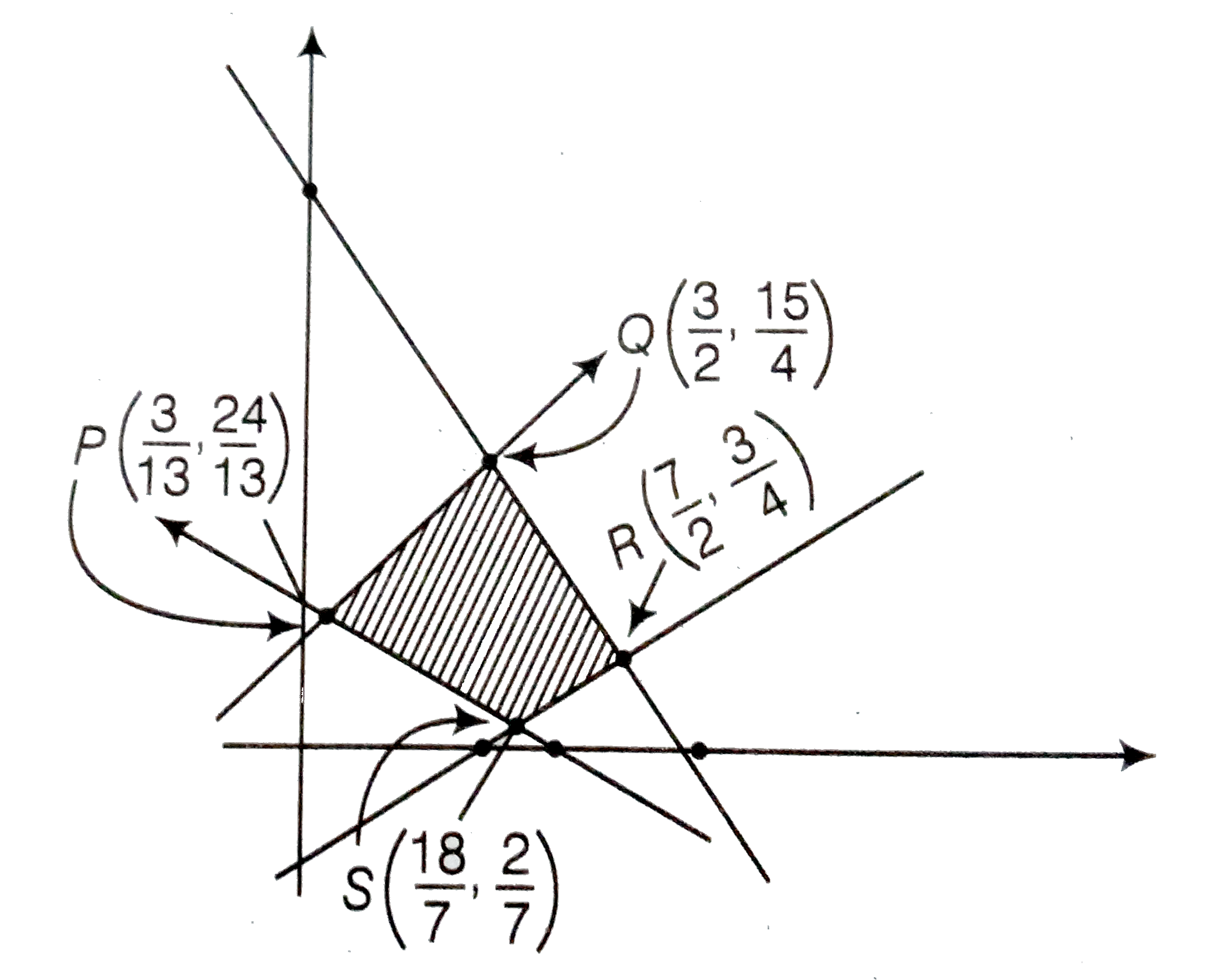 Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547
Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
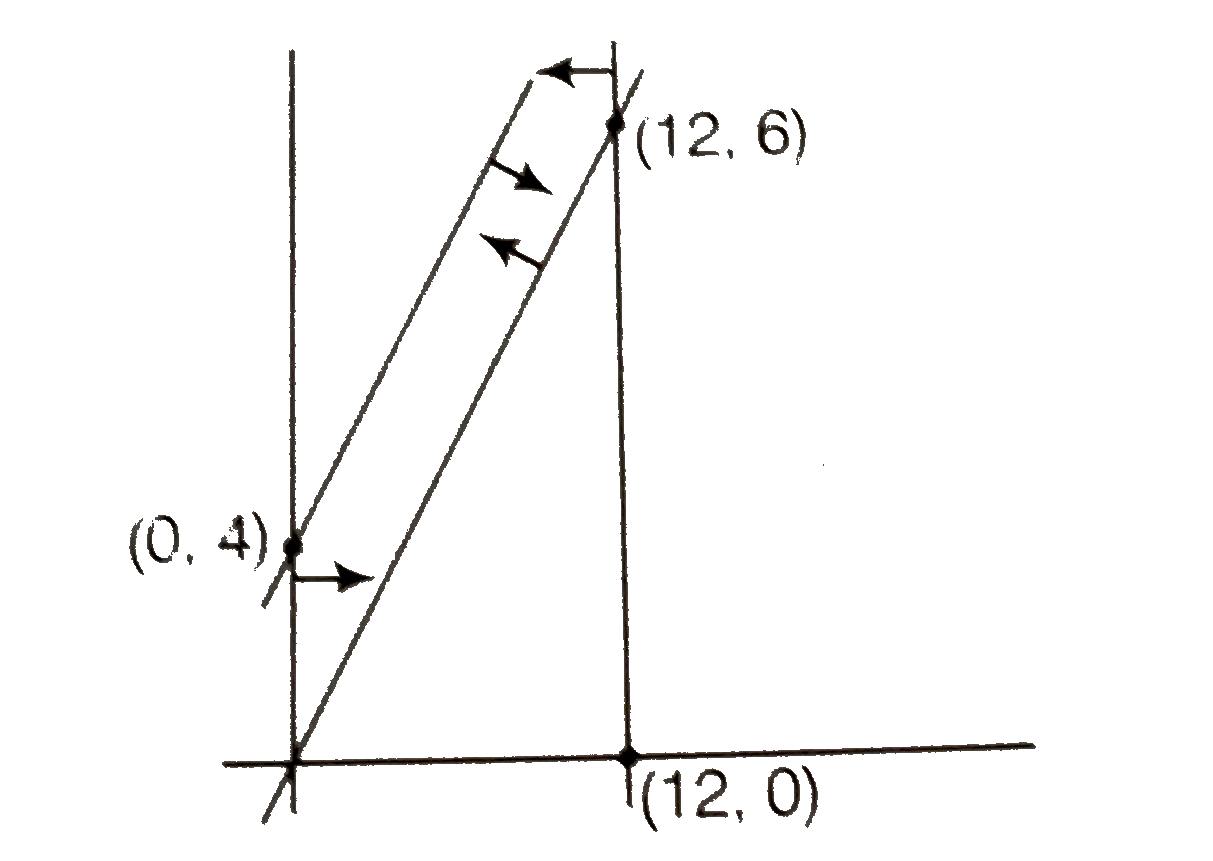 A0B8C12D−18
A0B8C12D−18
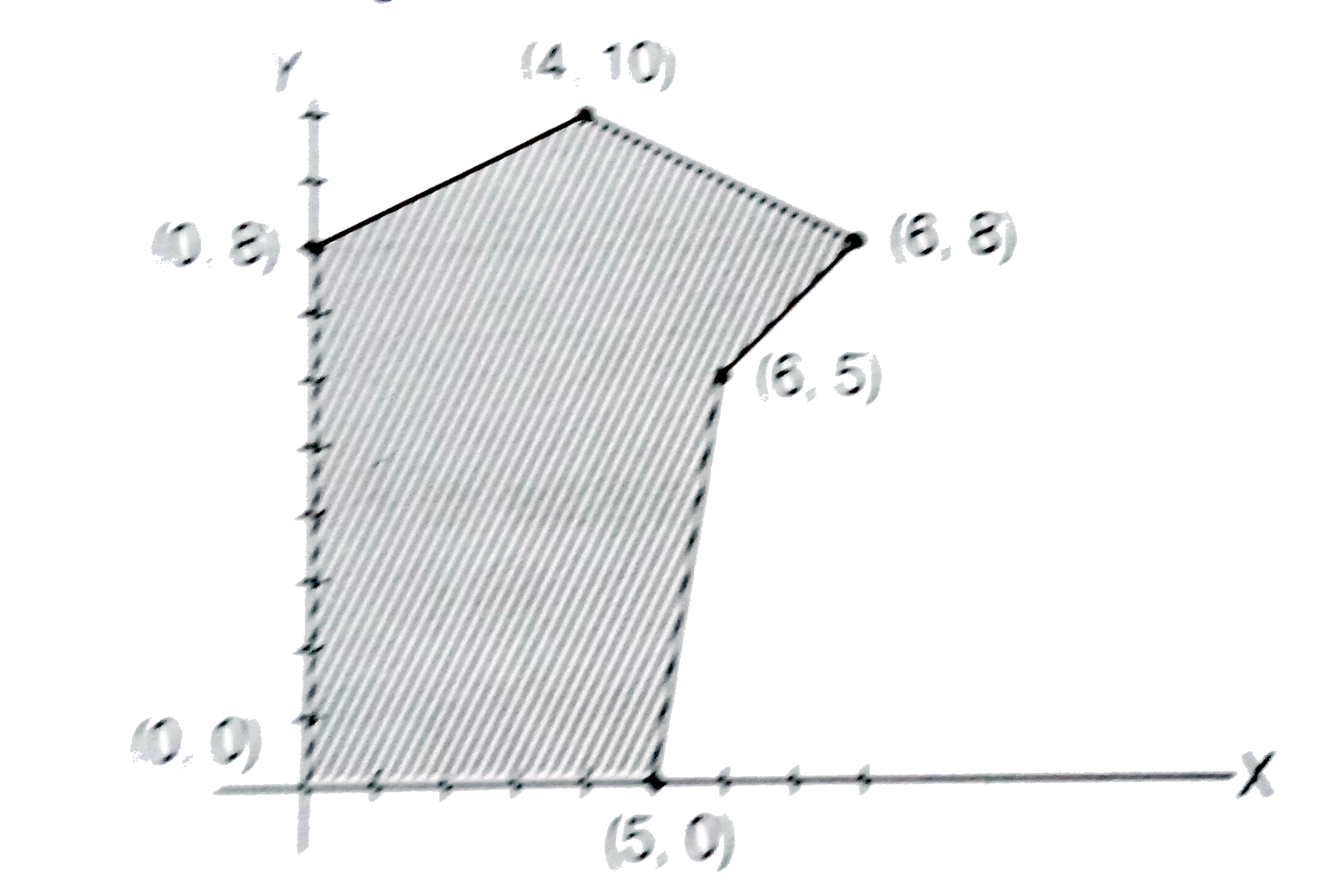
Feasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

View SolutionThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:

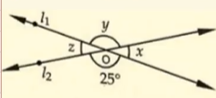
View SolutionIn Figure, find the value of x, y and z
View SolutionThe feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R1 is the feasible region, and the ojective function is Z1=2x−y, then the maximum value of Z1 occurs at:
View SolutionThe feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
View Solution


