The feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:

(3,2)
(4,0)
(6,0)
(0,3)
The correct Answer is:B
Step by step video & image solution for The feasible regions for two LPP is show in the following figure. Based on the given information, answer the following questions: If R_(2) is the feasible region and the objective function is Z_(2) = 4x + 3y, then the minimum value of Z_(2) occurs at: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
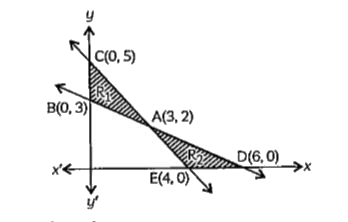
The feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R1 is the feasible region, and the ojective function is Z1=2x−y, then the maximum value of Z1 occurs at:
 View Solution
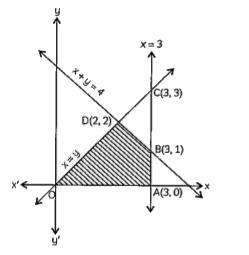
View SolutionIn the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
 View Solution
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 View Solution
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.
 View Solution
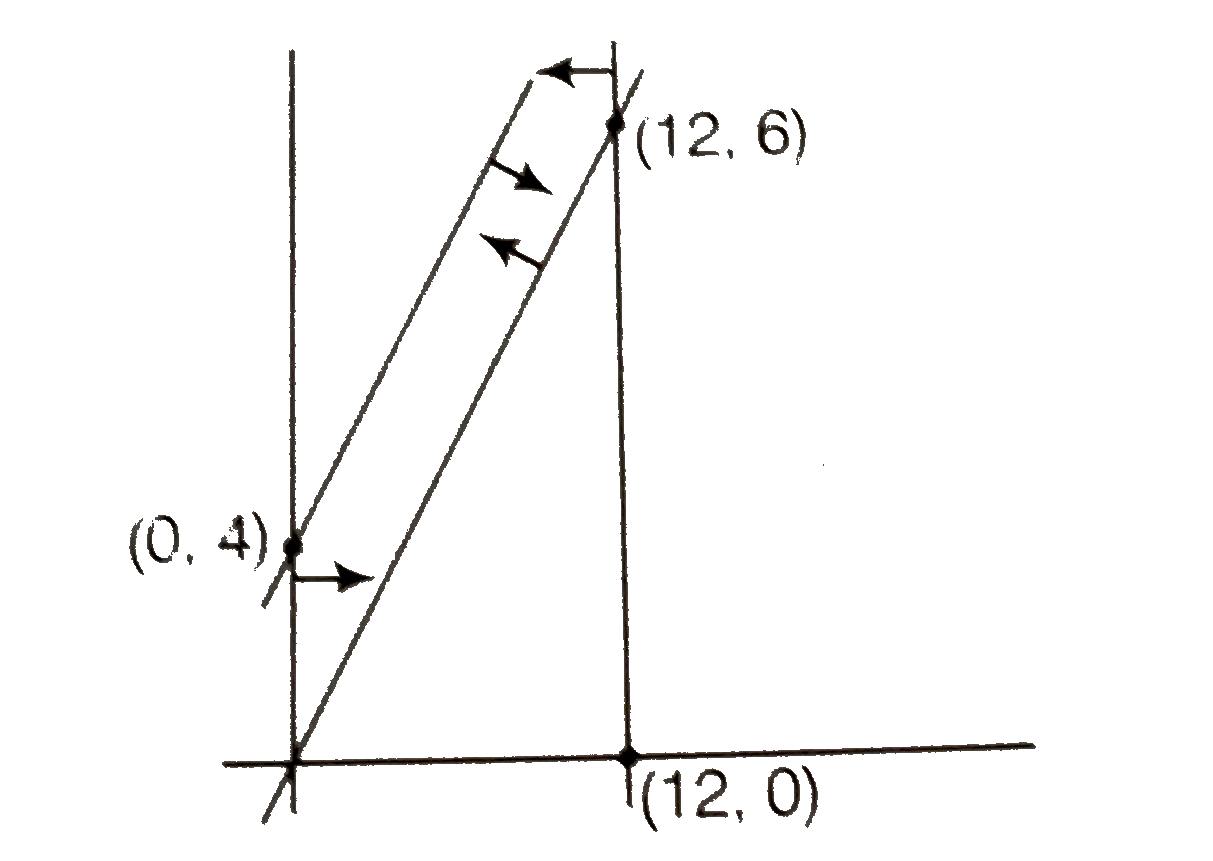
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
 View Solution
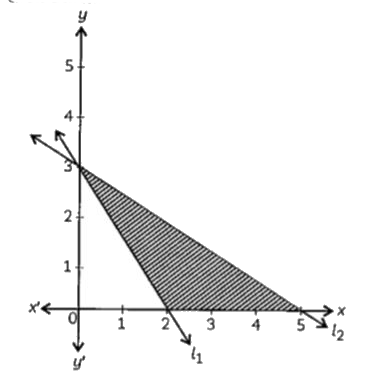
View SolutionThe feasible region of a sytem of linear inequations is shown below. If Z = 2x + y, then the minimum value of Z is:
 View Solution
View SolutionThe feasible region of an LPP is shown in the figure. If z=3x+9y ,then the minimum value of z occurs at
View SolutionIn the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
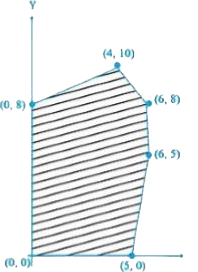 View Solution
View SolutionThe feasible region of a system of linear inequalities is shown below. If the objective function is maximise Z = 25x + 15y, then the maximum value of Z occurs at:
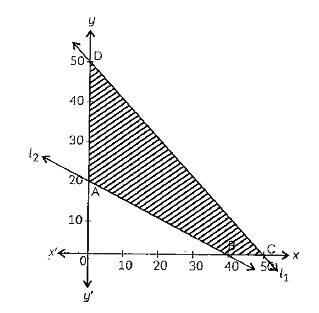 View Solution
View SolutionThe feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
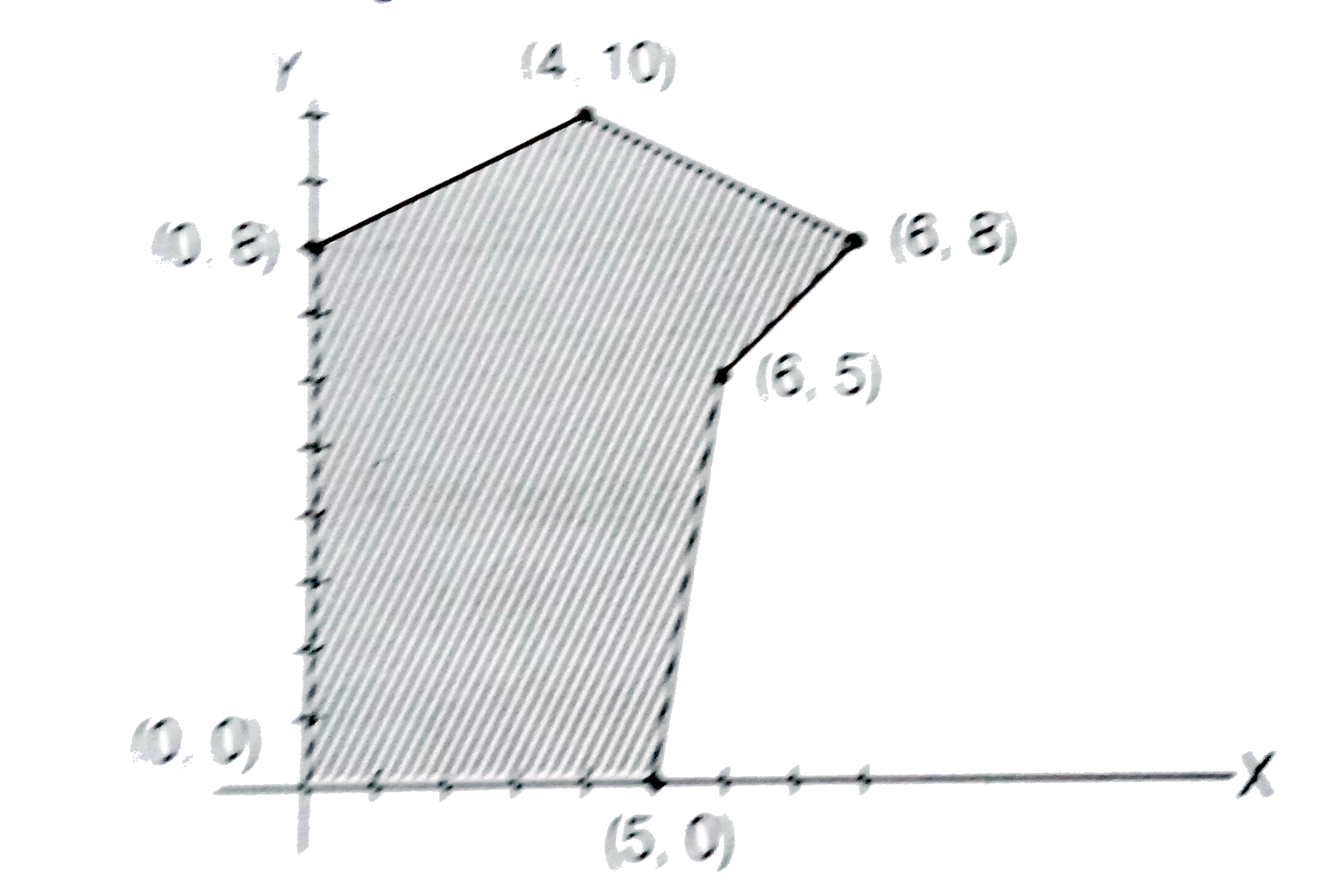 View Solution
View Solution


