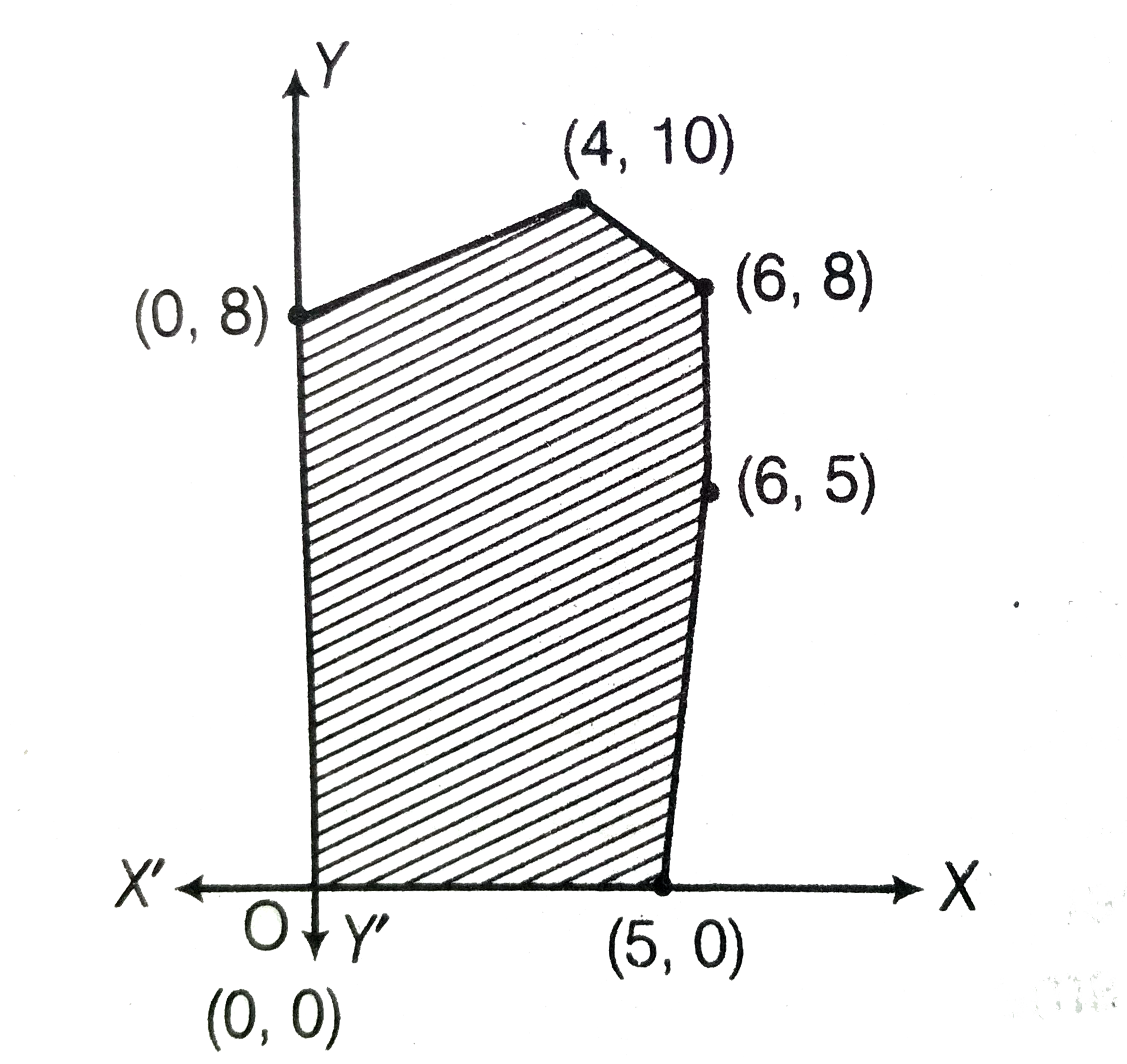
The feasible solution for a LPP is hown as below,
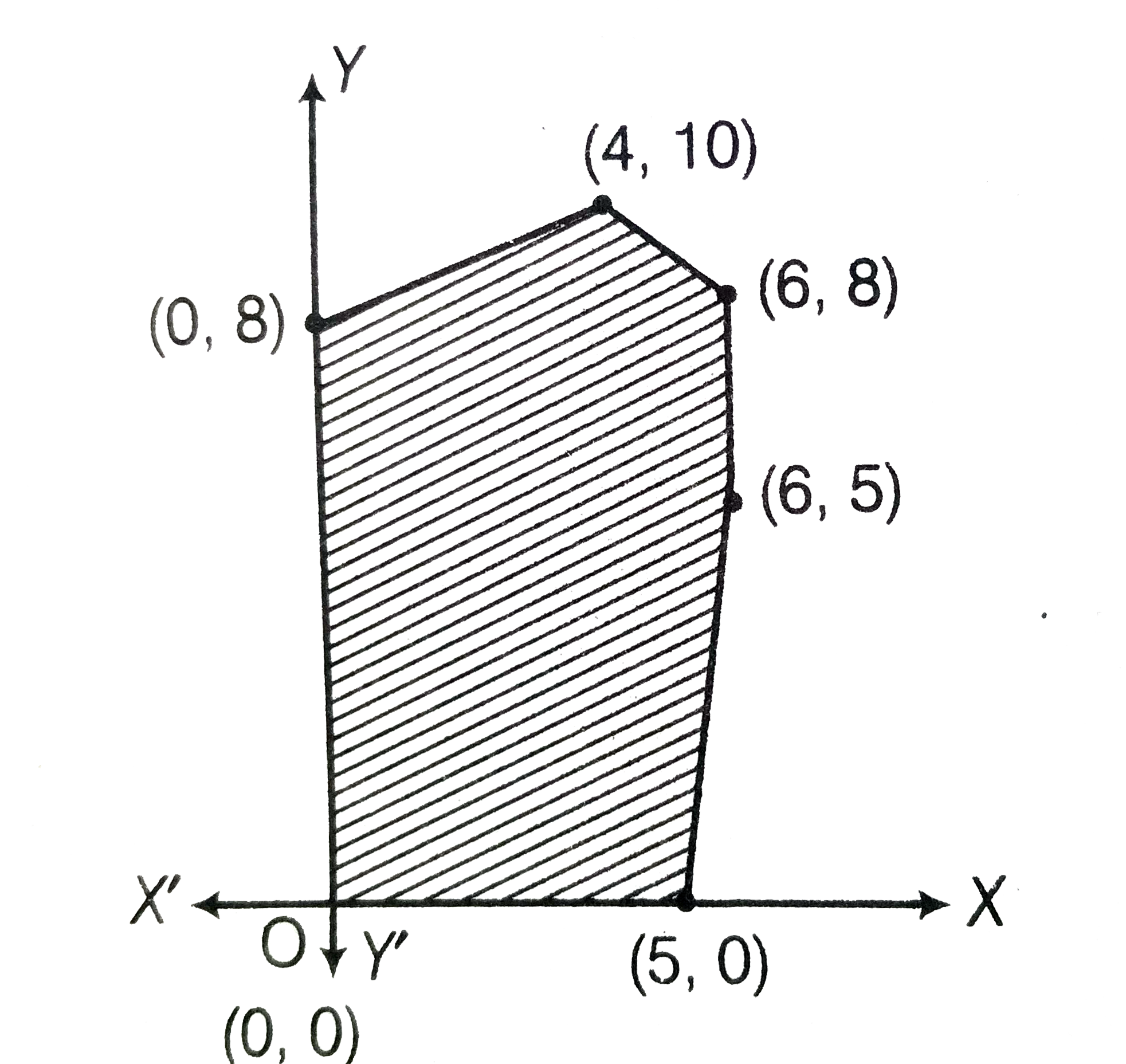
Let Z =3x -4y be the objective function . Then,
Maximum of Z occurs at
(5,0)
(6,5)
(6,8)
(4,10)
The correct Answer is:A
From the above table. The maximum value of Z is 15 which occurs at point (5, 0).
Topper's Solved these Questions
- Linear Programming Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:Linear Programming Exercise:EXERCISE 2 (MISCELLANEOUS PROBLEMS )
Explore 30 Videos
- Linear Programming Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:Linear Programming Exercise:MHT CET Corner
Explore 13 Videos
- Linear Programming Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:Linear Programming Exercise:MHT CET Corner
Explore 13 Videos
- LINEBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:LINEExercise:MHT CET Corner
Explore 3 Videos
- MATHEMATICAL LOGIC Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MATHEMATICAL LOGIC Exercise:MHT CET CORNER
Explore 22 Videos
Similar Questions
Knowledge Check
The feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
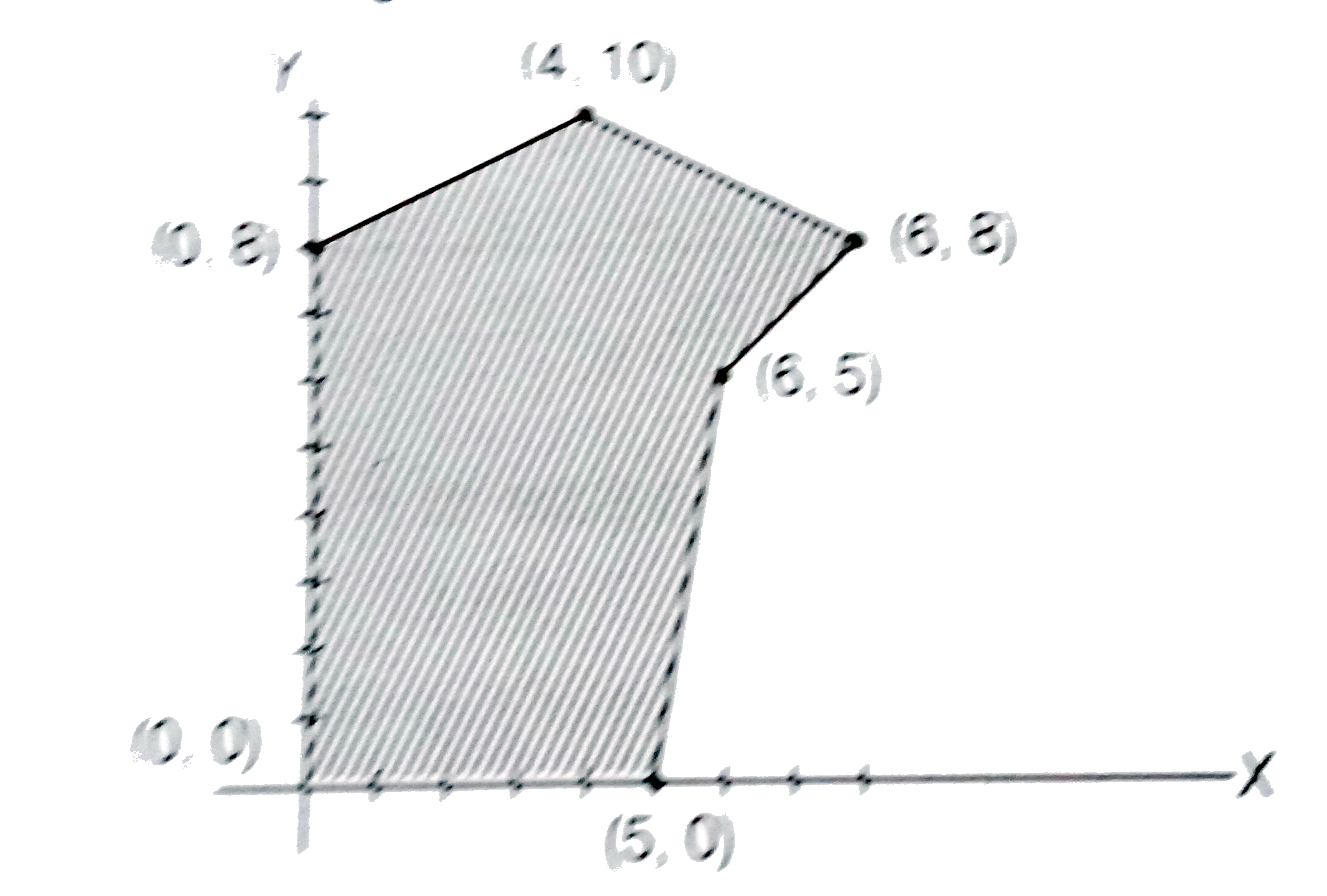 A(0,0)B(0,8)C(5,0)D(4,10)
A(0,0)B(0,8)C(5,0)D(4,10)The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
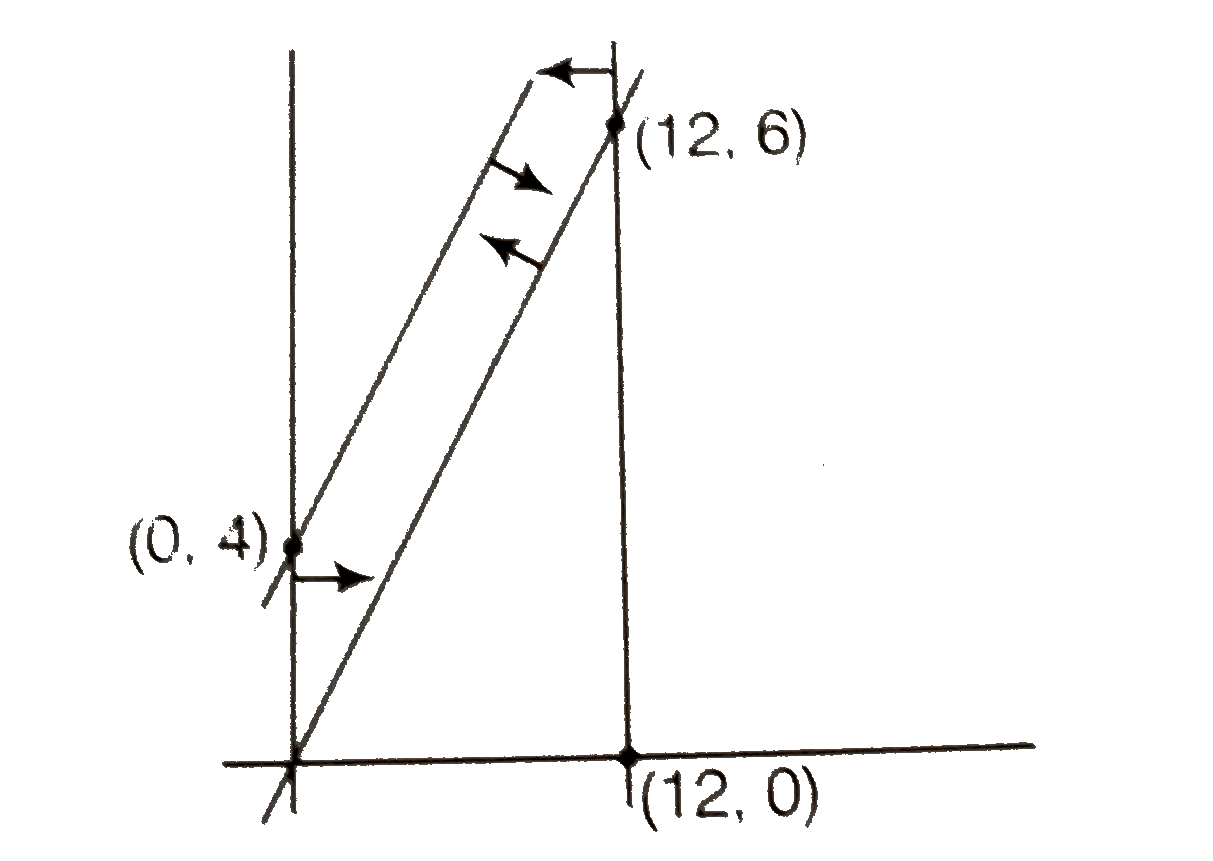 A0B8C12D−18
A0B8C12D−18Let R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
AWhen Z has an optimal value, where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region .BIf R is bounded, then the objective function Z has both a maximum and a minimum value on Rand each of these occurs at a corner point of R .CIf R is unbounded, then a maximum or a minimum value of the objective function may not existDIf R is unbounded and a maxil'TUJm or a minimum value of the objective function z exists, it must occur at corner point of R
The feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
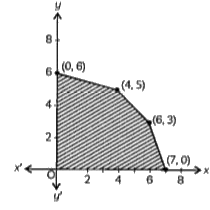
View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
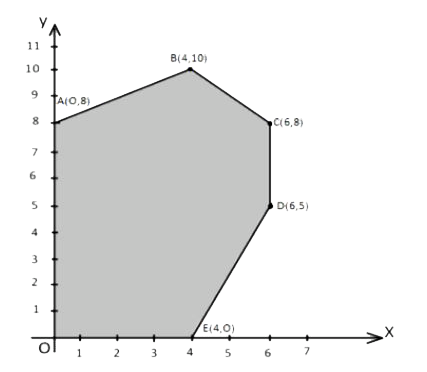
Let Z=3x−4y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionIf the feasibile region for a LPP is undoubed, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionCorner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F=4x+6y be the objective function. Determine the minimum value of F occurs at
View Solution