The area of the feasible region for the following constraints 3y+x≥3,x≥0,y≥0 will be

A

bounded

B

unbounded

C

convex

D

concave

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Given constraints are 3y+x≥3,x≥0,y≥0
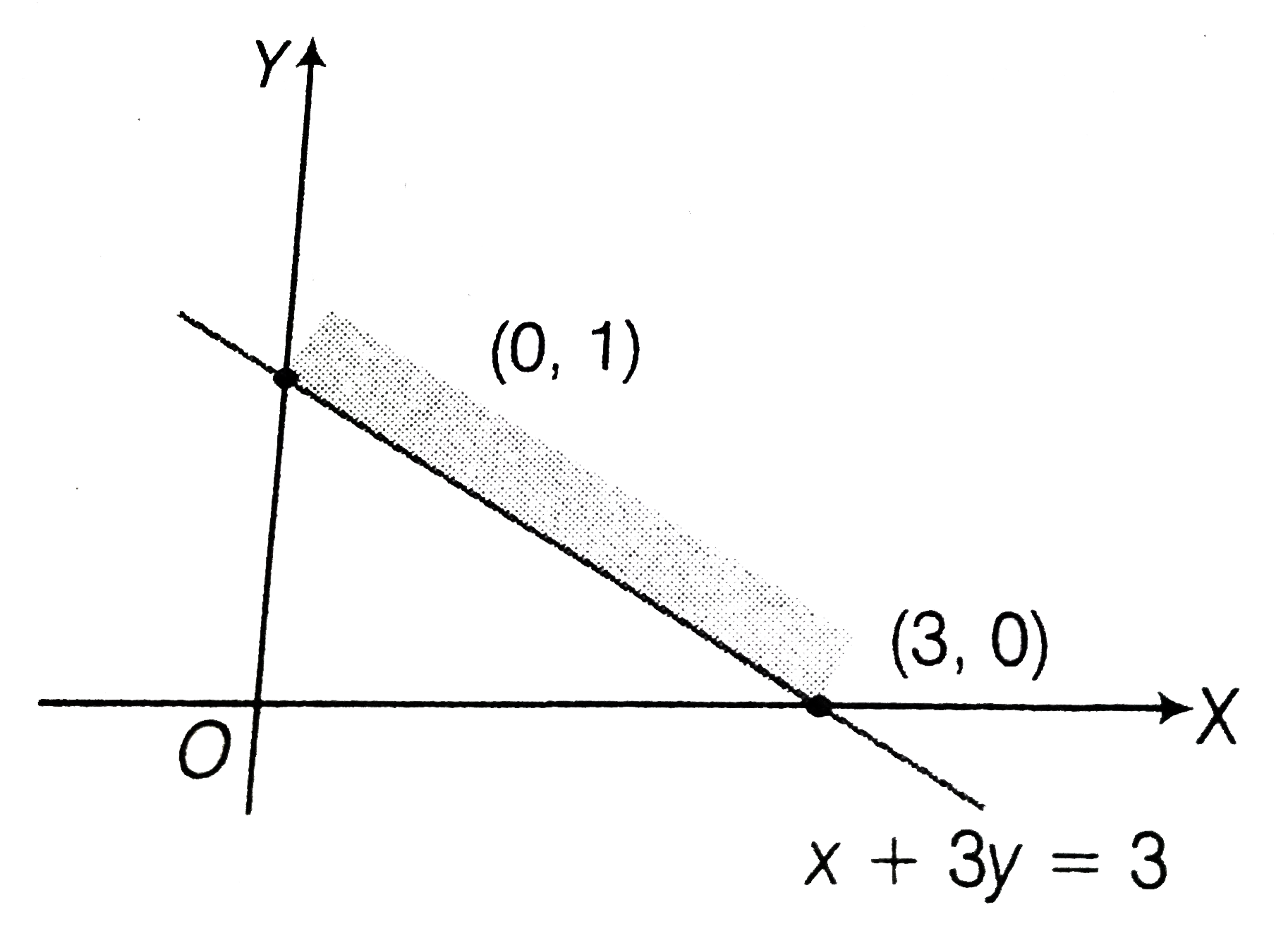
ocr_image
It is clear from the graph that feasible region is unbounded.

Updated on:21/07/2023
|
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The feasible region for the following constraints L1≤0,L2≥0,L3=0,x≥0,y≥0 in the diagram shown is
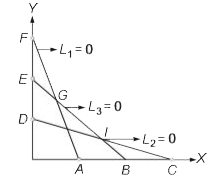    ocr_image

    Aarea DHF
    Barea AHC
    Cline segment EG
    Dline segment GI

  • The feasible region of a LPP under the constraints x−y≤1,x+y≥3,x≥0,y≥0

    Ais bounded and lies in first quadrant
    BIs unbounded and lies first quadrant
    Cdoes not exist
    Dis not in the first quadrant

  • The Corner points of feasible region for the inequations , x+y≤5,x+2y≤6,x≥0,y≥0 are

    A(0,3),(5,0),(0,5),(6,0)
    B(0,3),(5,0),(4,1),(0,0)
    C(0,0),(1,4),(5,0),(0,3)
    D(3,0),(0,5)(0,0),(4,1)