The minimum value of the objective function Z=2x+10y for linear constraints x≥0,y≥0,x−y≥0,x−5y≤−5 is
10
15
12
8
The correct Answer is:B
Given Z=2x +10 y
Here, feasible region is undbounded .
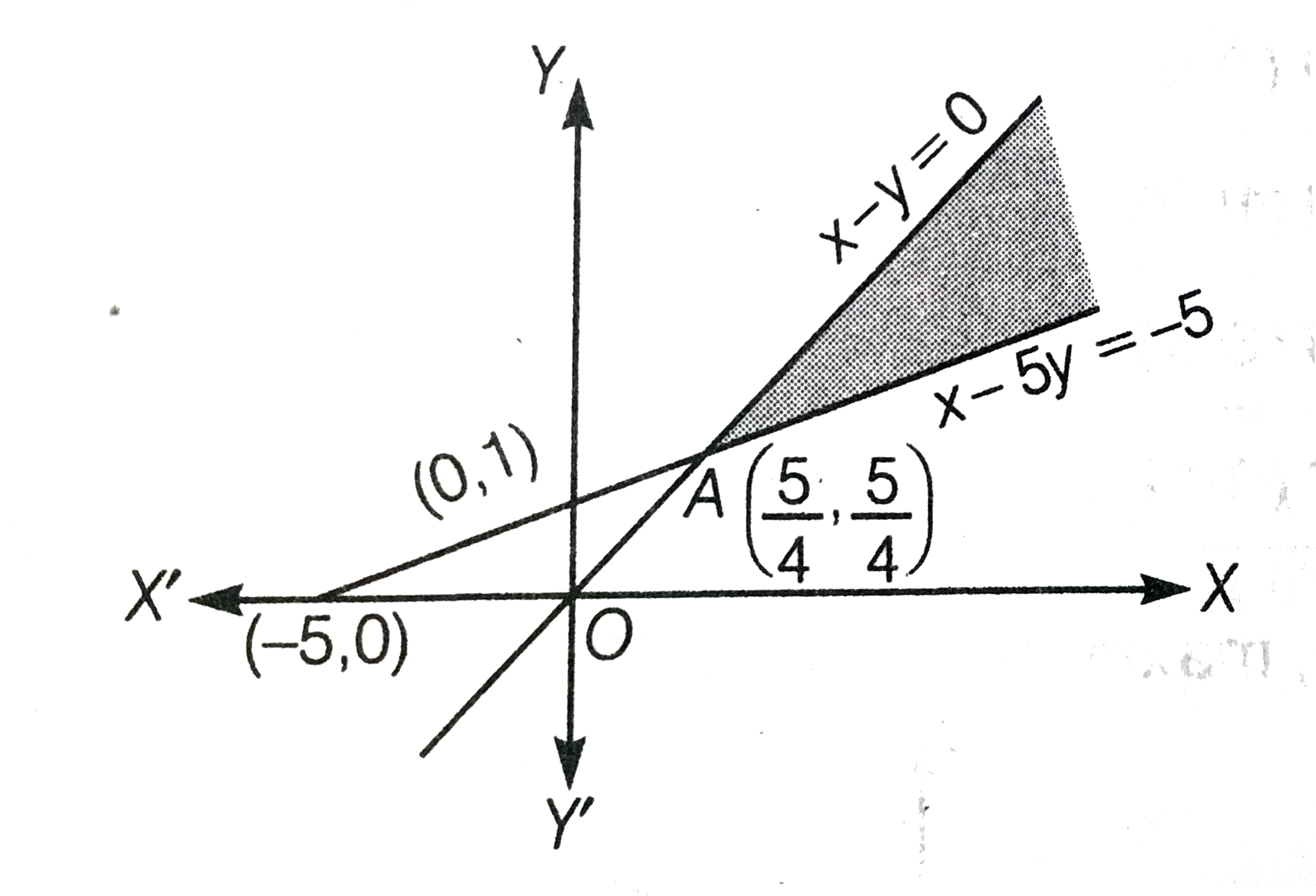
At point A(54,54),Z=2(54)+10(54)=15
Now, this value of Z may be minimum value. We see that half plane determined by 2x + 1 Oy lt 15 has no point in common with the feasible region . So, Z has minimum value 15.
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Find the ratio of the maximum and minimum values of the objective function f=3x+5y subject to the constraints : x≥0,y≥0,2x+3y≥6and9x+10y≤90.
View SolutionDetermine graphically the minimum value of the objective function: Z=−50x+20y subject to the constraints:
2x−y≥−5,3x+y≥3,2x−3y≤12,x,y≥0.
View Solution
Knowledge Check
The maximum value of the objective function Z=3x+2y for linear constraints x+y≤7,2x+3y≤16,x≥0,y≥0 is
A16B21C25D28The minimum and maximum values of the objective function, Z = 5x + 10y subject to the constraints x+2y≤120,x+y≥60,x−2y≥0,x,y≤0 are respectively
A300 and 500B600 and 700C600 and 700D300 and 400The minimum value of the objective function Z=x+2y
Subject to the constraints,
2x+y≥3,x+2y≥6,x,y≥0 occursAat every point on the line x + 2y = 6Bat every point on the line 2x + y = 3Cat every point on the line x + 2y = 3 dDat every point on the line 2x + y = 6
Determine graphically the minimum value of the objective function z = - 50x + 20 y, subject to he constraints.
2x−y≥−5
3x+y≥3
2x−3y≤12
x≥0,y≥0
View SolutionThe minimum value of linear objective function z =2x + 2y under linear constraints 3x+2y≥12,x+3y≥11andx,y≥0 is
View SolutionThe maximum and minimum values of the objective function Z = x + 2y subject to the constraints
x+2y≥100,2x−y≤0,2x+y≤200 occurs respectively at
View SolutionThe objective function Z=30x+20y, subject to constraints x+y≤8,x+2y≥4,6x+4y≥12,x≥0,y≥0, has
View SolutionThe minimum value of Z=4x+5y subjected to the constraints x+y≥6,5x+y≥10,x≥0,y≥0 is
View Solution
