Consider the linear programming problem Maximise Z = 4x + y.
Subject to constraints $x + y \leq 50, x + y \geq 100$ and $x, y \geq 0$ Then, maximum vlaue of Z is

A

0

B

50

C

100

D

does not exist

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given, maximise , Z= 4x+y and constraints are $x + y \leq 50, x + y \geq 100, x y \geq 0$

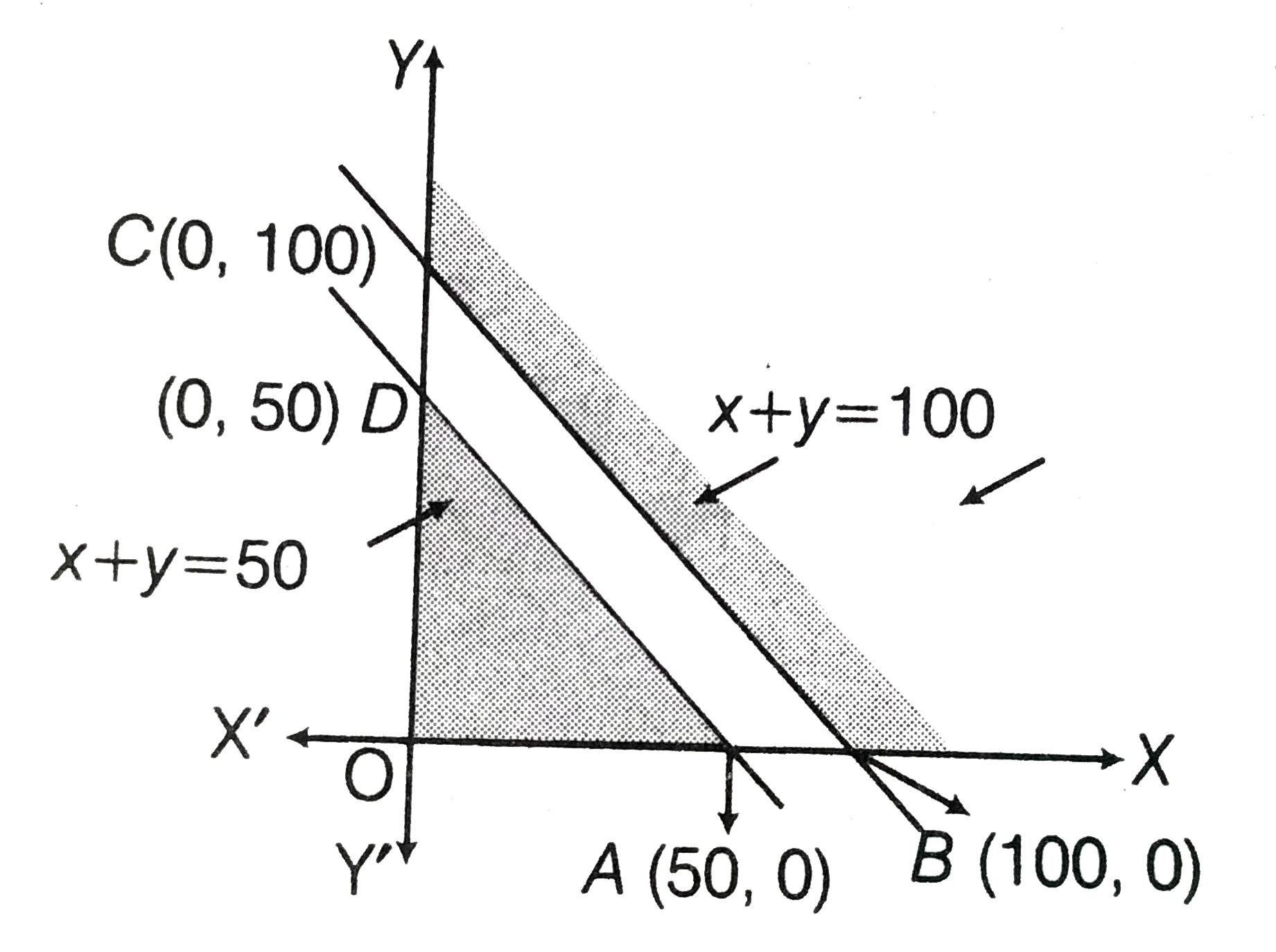
It is clear from the graph that, there is no feasible reg.ion, so maximum value cannot be determined.

|

Updated on:21/07/2023

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Solve the linear programming problem. Maximise Z = x + 2y
Subject to constraints $x - y \leq 10, 2 x + 3 y \leq 20$ and $x \geq 0, y \geq 0$
AZ=10
BZ=30
CZ=40
DNone of these
Question 2 - Select One
The maximum value of Z = 4x + 2y subject to the constraints $2 x + 3 y \leq 18, x + y \geq 10, x, y \geq 0$ is
A20
B36
C40
DNone of these
Question 3 - Select One
The linear programming problem minimiseZ=3x+2y subject to the constraints
$x + y \geq 8$
$3 x + 5 y \leq 15$
$x \geq 0, y \geq 0$ has
Aone solution
Bno feasible solution
Ctwo solutions
Dinfinitely many solution

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-Linear Programming -EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method )

Home
Ask Doubt
Profile