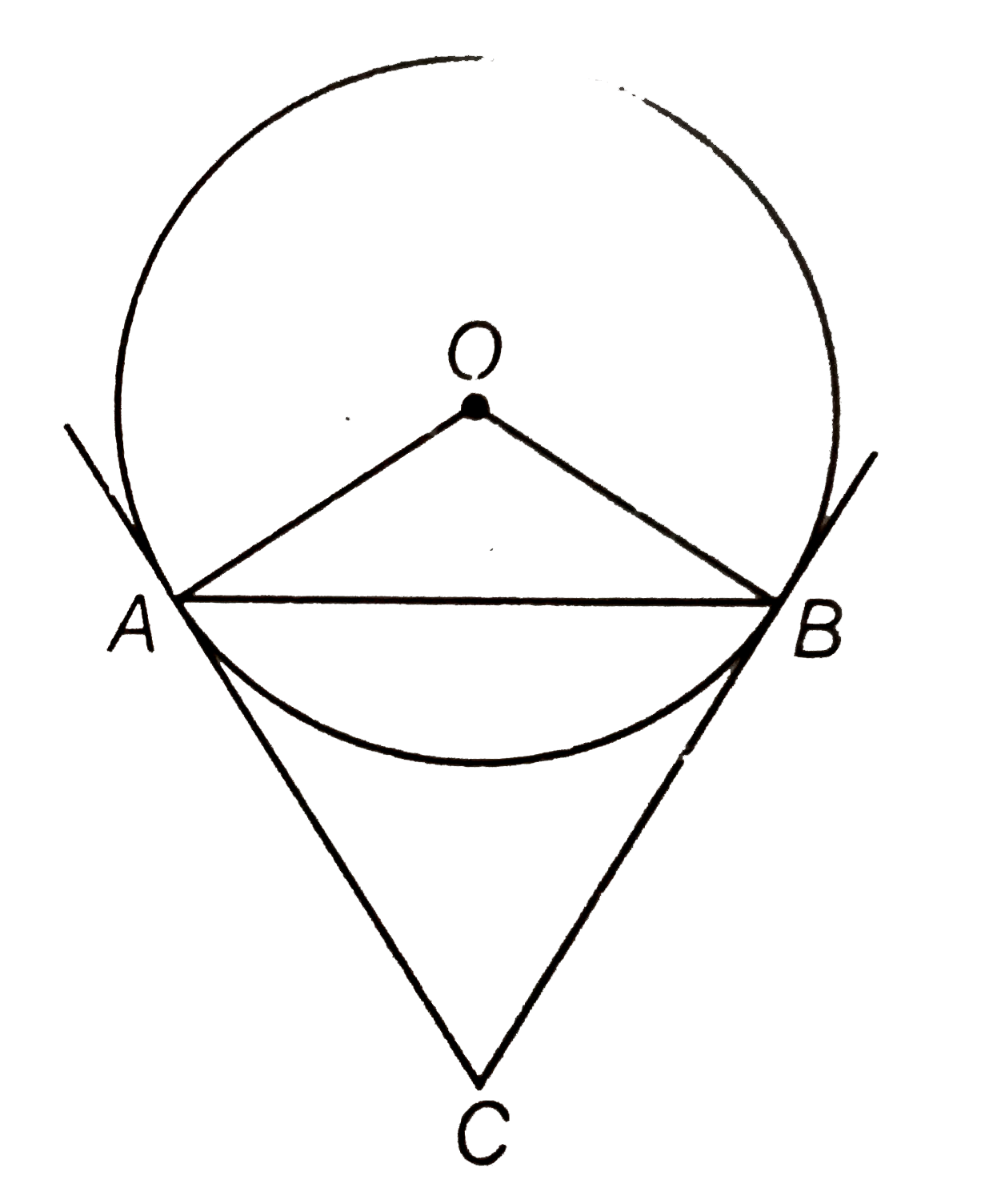
If a chord $A B$ subtends and angle of $60^{\circ}$ at the centre of a circle, then the angle between the tangents to the circle drawn from $A$ and $B$ is

Video Solution

Text Solution

Verified by Experts

Since a chord AB subtends an angle of $60^{\circ}$ at the centre of a circle.
i.e., $∠ A O B = 60^{\circ}$
As OA = OB= Radius of the circle
$∠ A O B = 60^{\circ}$
The tangent at pionts A and B is drawn, which intersect at C.
We know, $O A ⊥ A C and O B ⊥ B C$ .
$∴ ∠ O A C = 90^{\circ}, ∠ O B C = 90^{\circ}$
$\Rightarrow ∠ O A B + ∠ B A C = 90^{\circ}$
and $\Rightarrow ∠ O B A + ∠ A B C = 90^{\circ}$ $\Rightarrow ∠ B A C = 90^{\circ} - 60^{\circ} = 30^{\circ}$
and $\Rightarrow ∠ A B C = 90^{\circ} - 60^{\circ} = 30^{\circ}$
In $Δ A B C$ , $∠ B A C + ∠ C B A + ∠ A C B = 180^{\circ}$
[since, sum of all interior angles of a triangle is $180^{\circ}$ ]
$\Rightarrow ∠ A C B = 180^{\circ} - (30^{\circ} + 30^{\circ}) = 120^{\circ}$

Updated on:21/07/2023

A chord of length 7 cm subtends an angle of $60^{\circ}$ at the centre of a circle. What is the radius (in cm) of the circle?
A $7 \sqrt{2}$
B $7 \sqrt{3}$
C $7$
D $14$
A chord of length 7 cm subtends an angle of $60^{\circ}$ at the centre of a circle. What is the radius (in cm) of the circle?
A $7 \sqrt{2}$
B $7 \sqrt{3}$
C $7$
D $14$
If a chord of a circle subtends an angle of $30^{\circ}$ at the circumference of the circle, then what is the ratio of the radius of the circle and the length of the chord respectively?
A $1 : 1$
B $2 : 1$
C $3 : 1$
D $\sqrt{2} : 1$